💣 Dyna

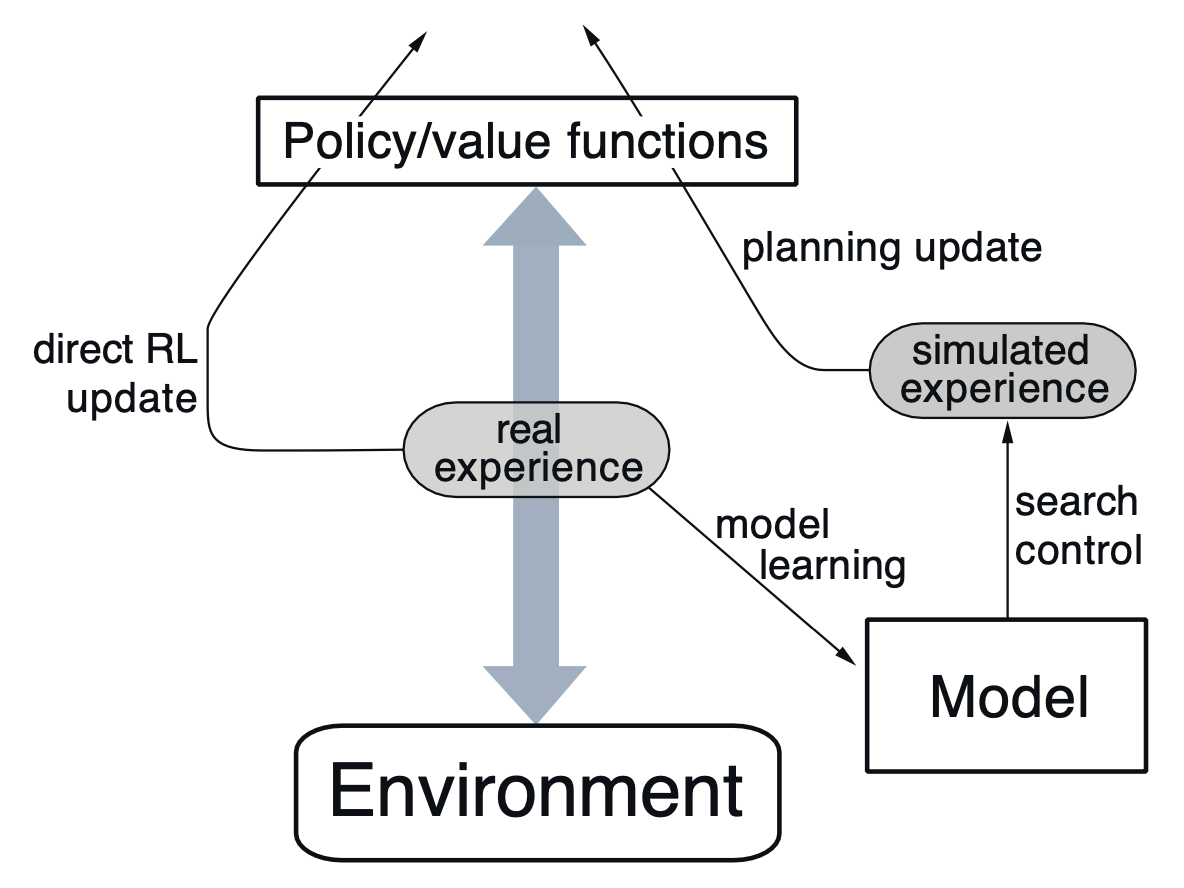
Dyna is a class of reinforcement learning algorithms that bridge model-free and model-based learning. It uses a learning algorithm that takes experiences from both the environment and the model simulation, thereby presenting two separate paths for learning—one directly through experience and one indirectly through model learning and planning.

Dyna-Q §

One prominent example of this class is Dyna-Q, a 🚀 Q-Learning-inspired algorithm. It augments the standard Q-learning updates via samples from the environment model, thus encouraging faster convergence.

The algorithm is as follows:

1. Given state , pick action with 💰 Epsilon-Greedy and observe .
2. Update model and using our transition. If our model is deterministic, our update is simply

3. Perform the Q-update using our immediate experience,

4. Repeat times:
   1. Sample from a buffer of past states.
   2. Simulate action on state via our model,

3. Perform another Q-update with our simulated experience, 

Model Updates §

If our environment is non-stationary, we would need to continuously update our model. Usually, this happens when our inaccurate model leads to an suboptimal policy that goes to some overestimated state; experiencing the actual value then corrects the error in our model.

A more general solution would be to directly encourage exploration. One method, similar to 🤩 Optimistic Exploration, is to track “time since last visit” for each transition. Then, we can augment our rewards by adding a small bonus dependent on this record, which encourages our algorithm to revisit transitions that haven’t been seen in a while.

Prioritized Sweeping §

Dyna-Q selects pairs from our buffer randomly. However, some updates are more helpful than others. Specifically, the priority of a state should depend on the magnitude of the induced update in our Q-function; the bigger the update, the more likely we should sample it.

Prioritized sweeping is an upgrade to the buffer selection process that maintains a 🔑 Priority Queue with the key being the update magnitude. Specifically, we replace the final simulated experience step with the following:

1. Take from the top of our priority queue.
2. Simulate action , observe , and perform Q-update

3. Using our model, check all that lead to :
   1. Compute , the predicted reward for action in , and compute the update magnitude

2. If $p$ is above some threshold, insert $(\bar{s}, \bar{a})$ into the priority queue with key $p$.