⚽️ Regularization Penalties

Regularization penalties force weights to be smaller, preventing over-reliance on certain features in the training data and therefore preventing overfitting.

Penalties commonly use 📌 Norms on the weights scaled by a strength coefficient, adding to the loss function.

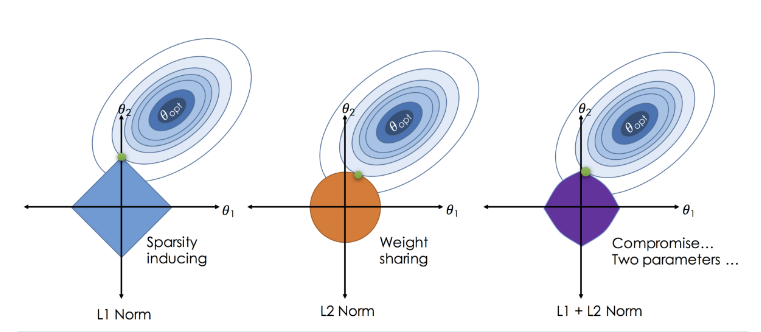
1. Ridge regression uses norm, which encourages all weights to be smaller and shrinks larger weights the most. This is equivalent to applying MAP in 🏦 Linear Regression.
2. Lasso regression uses norm, which evenly shrinks all weights and drives some to , performing feature selection. Optimization requires ⛰️ Gradient Descent.
3. With norm, we get a penalty that only cares about how many weights are , again performing feature selection, which is optimized with 🔎 Greedy Search.

The following is an example of how 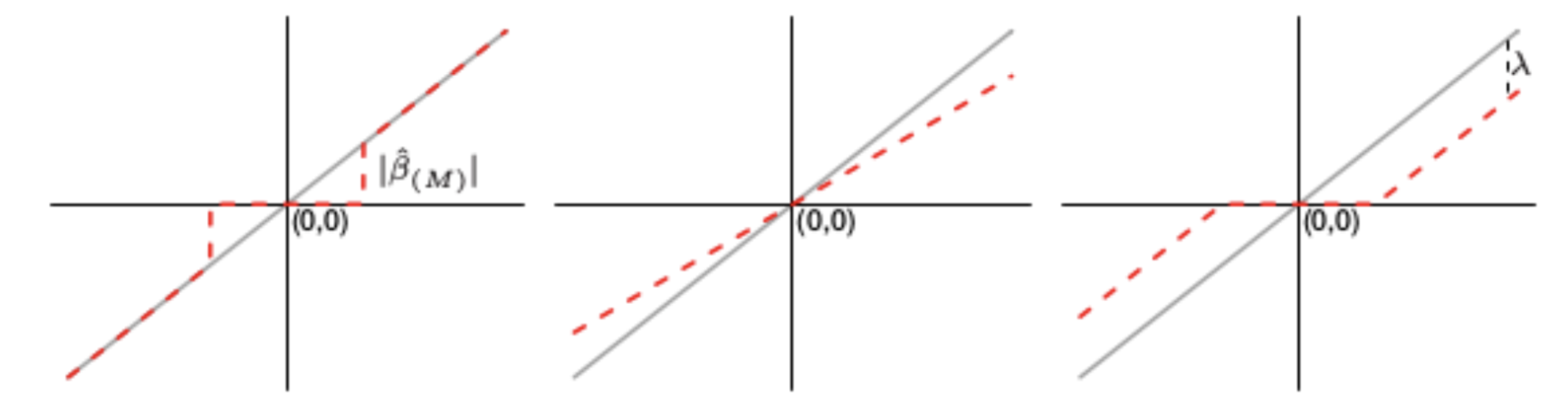, Ridge, and Lasso shrink a hyperparameter’s values. X-axis is the original value, and Y-axis is the new value.

Elastic-net uses both and loss, which shrinks large weights and feature selects at the same time.

The following is a visual example of the difference between Lasso, Ridge, and Elastic-net. The rings represent contours of the loss function, and colored shapes are contours of the penalty; their intersection is the optimal parameter setting.