📍 Epipolar Geometry

Epipolar geometry describes the relationship between two cameras in stereo vision (like the arrangement below).

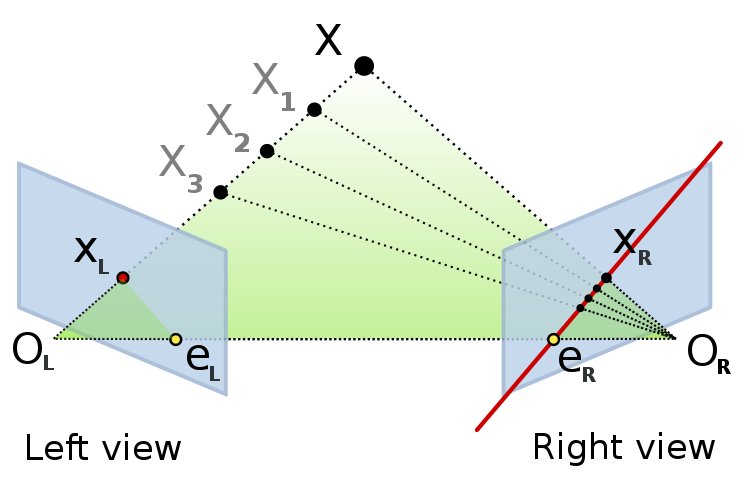
Epipolar Constraint §

In this setup, the green triangle forms a plane called the epipolar plane. Let and be the calibrated coordinates of in the left and right camera coordinate systems respectively. If and are the rotation and translation from the left camera to the right, the sides of the triangle are scaled versions of , , and (left, right, bottom sides).

Since these three vectors lie on the same plane, we get the epipolar constraint

Geometrically, this says that the vector orthogonal to and (the cross product) is orthogonal to (via the dot product evaluating to zero).

Epipolar Line §

The intersection of the epipolar plane with the image plane gives us the epipolar line. To find the equation of this line, we can rearrange the epipolar constraint for each view.

For the left image, we have

where the left epipolar line is

For the right image, we have

where the right epipolar line is

Epipole §

The intersection of all epipolar lines (from multiple correspondences) in an image plane is called the epipole. The epipole is also the projected location of one camera center onto the other’s camera plane.

Geometrically, varying and shifts the left and right sides of the triangle, but the bottom (defined by ) is kept constant. Thus, we can see that the epipole must lie on the bottom side for each image plane; that is, our epipoles