👁️ Convolutional Neural Network

For some tasks, we don’t need each neuron to take in all outputs from the previous layer, as seen in a 🕸️ Multilayer Perceptron; local receptive fields limits a neuron’s inputs to nearby neurons.

Convolutional neural networks (CNNs) apply this idea in 2D; instead of a flat layer of neurons, each convolutional layer consists of a structured 3D tensor consisting of multiple 2D matrices. Below is an illustration of this structure.

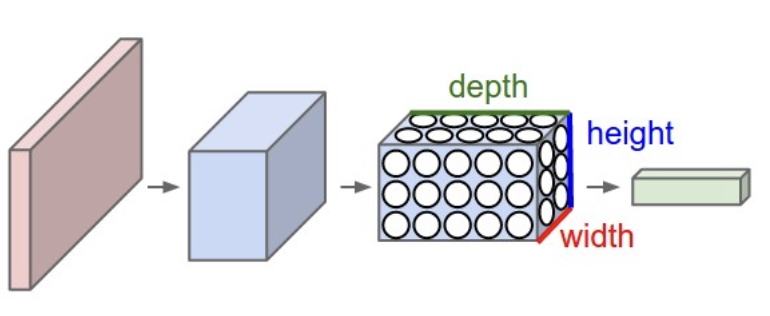
Each layer has multiple 3D filters, defined by its dimensions, stride, and padding; each filter consists of weights, and we convolve these filters with the activations of the previous layer (see ♻️ Convolution). One filter results in one 2D matrix, and stacking these matrices gives us the 3D tensor.

Max Pool §

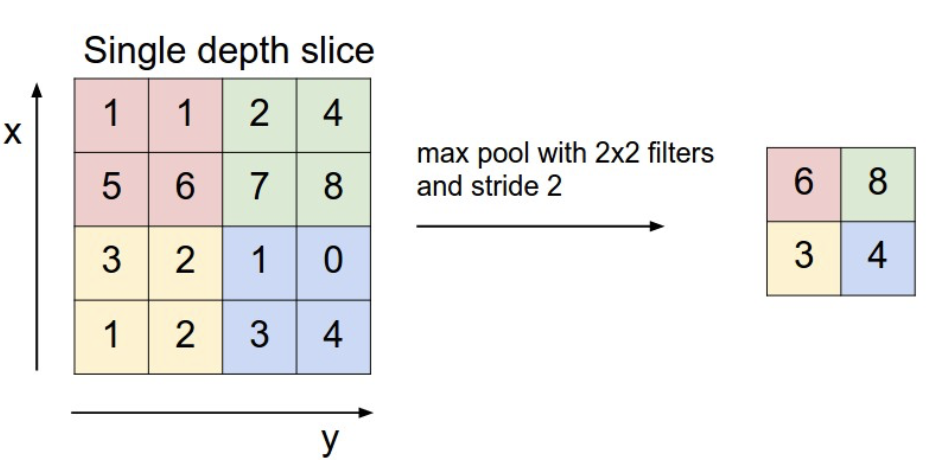
Max pool layers are used to reduce the first two dimensions of a 3D tensor, partitioning the input and getting the maximum value for each. Note that we use maximum instead of average because most of the input is zero, and we want to capture strong activations instead of muddying the signals with an average.

The max pool serves as dimension reduction and prevents overfitting. Below is an example.

Model §

CNN consists of convolution, max pool, and dense layers; max pools usually go between convolutions, and for unstructured labels , we flatten the 3D tensor near the end and pass it through dense layers before the final output.

For structured outputs, we don’t use dense layers.

Info

Due to using convolutions instead of dense layers, CNNs usually have much fewer weights than it would have if it used dense layers instead.

Equivariance and Invariance §

Crucially, the convolution operation maintains translation 🪞 Equivariance—if we translate our input, the output is also translated. This encodes the key assumption that CNNs make: any translated version of our image is similar to the original.

Though the individual convolution operation is equivariant, our entire CNN applies other layers as well (like max pooling or flattening). As a result, the entire network has translation 🗿Invariance—if we translate the input, our output will stay (approximately) the same.

Due to this invariance, significant data augmentation techniques can be used to increase our dataset size. Common strategies include flipping the image, slightly cropping the image or translating it, or applying a color filter.