⌛️ Temporal Convolutional Networks

Temporal convolutional networks (TCNs) is a class of networks that apply convolutions from 👁️ Convolutional Neural Networks to sequence modeling. Our problem is to predict some sequence

with a function and the causal constraint that depends only on .

To achieve this, we can apply 1D convolutions along the sequence’s time dimension with padding to ensure that the intermediate and final layers have the same size as the input. Furthermore, in order to maintain the causal constraint, we can use causal convolutions that simply shift the convolution output to the farthest time in the convolution’s window.

However, this naive approach has a receptive field that’s solely defined by the depth of the network. To widen this field, we can use dilated convolutions defined as

where , our dilation factor, controls the “skips” in between the convolution input and is the convolution size. Moreover, to stabilize deep networks, we also use residual connections (from 🪜 ResNet). Combining these enhancements with the ingredients above gives us the generic TCN architecture pictured below (dilated convolutions on left, residual connections in middle, and combining them on the right).

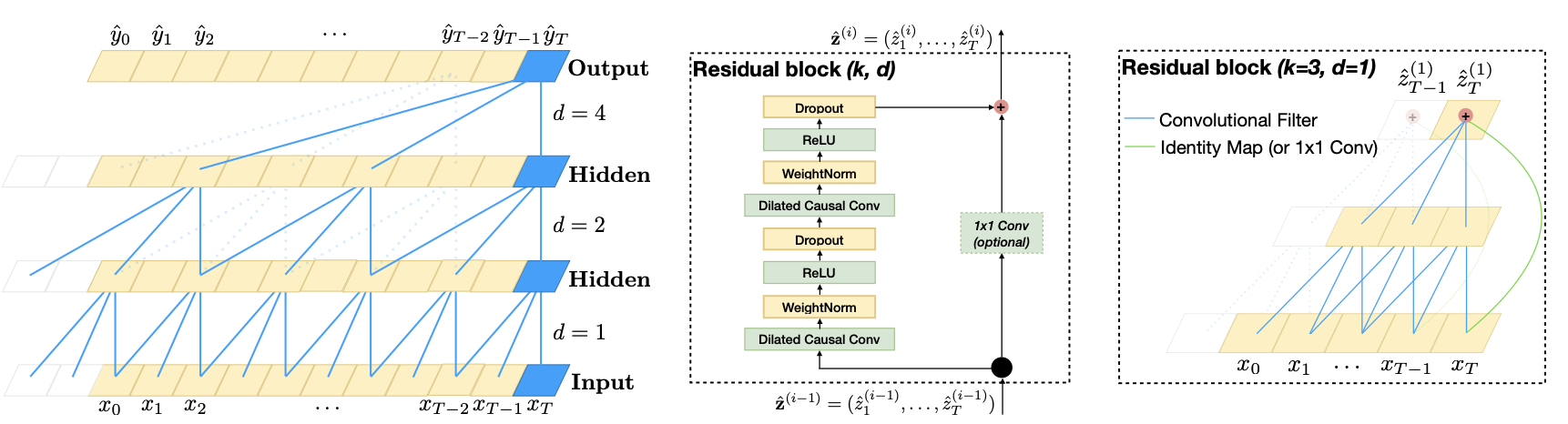
Unlike 💬 Recurrent Neural Networks, TCNs enforce a fixed history (input sequence) size and enable parallelism. One key advantage of this structure is that gradient are propagated through the hidden layers rather than through the temporal dimension, thus avoiding the RNN’s infamous exploding and vanishing gradients.