The score SDE, a time-dependent score-based model, seeks to learn the score of the data distribution. This is an extension of the 🎧 NCSN into infinitesimally small noise-scale steps. This model also shares heavy resemblances to 🕯️ Diffusion Probabilistic Models.
SDE Perturbation
Let
where
As
SDE Reversal
To recover our data distribution from
The time-dependent score-based model seeks to learn this score,
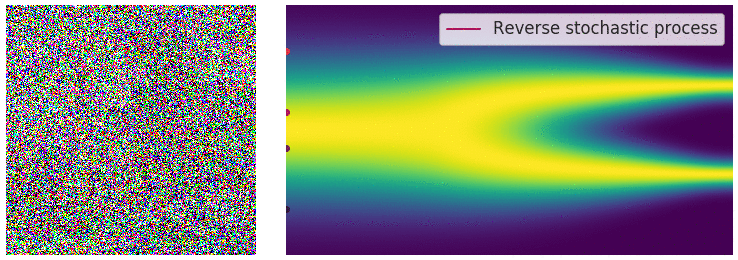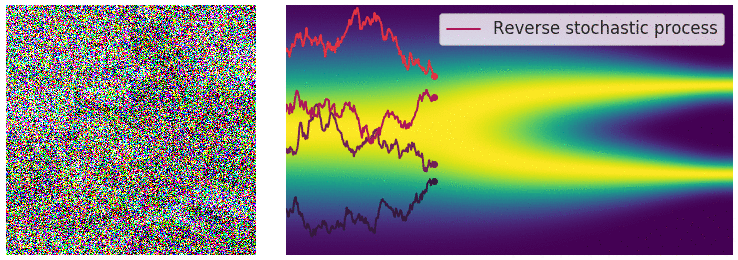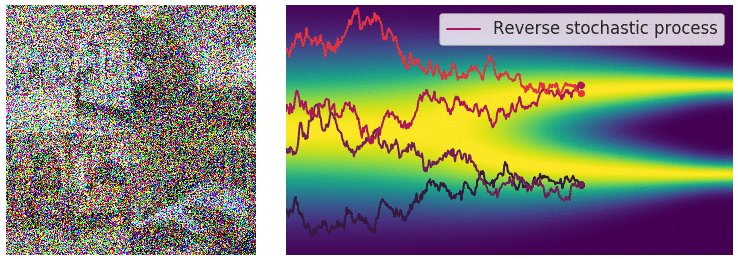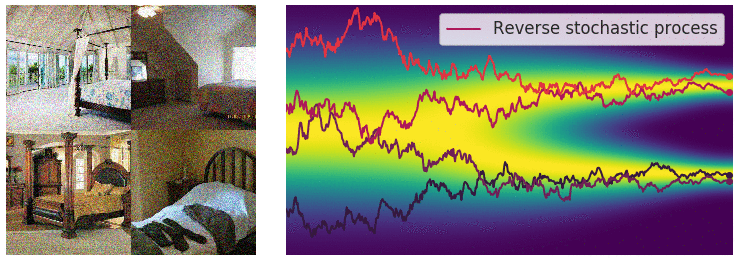
Optimization
We follow a similar setup from NCSN, training
with
Predictor-Corrector
To computationally solve the reverse SDE, we can use the Euler-Maruyama method, which quantizes time
This can be improved via fine-tuning with 🎯 Markov Chain Monte Carlo. The predictor is a SDE solver like Euler-Maruyama that predicts the next step
With this method, we can achieve incredibly realistic samples from our modeled distribution.
Probability Flow ODE
One limitation of the SDE method is that we can’t compute the log likelihood of our model. Fortunately, we can convert the SDE to an ordinary differential equation
This resembles a 🎱 Neural ODE, which thus allows us to compute the exact log likelihood.