☂️ Hidden Markov Model

Hidden Markov models are a common structure for ⏰ Dynamic Bayesian Networks that model probability distribution with the Markov property, which states that each variable conditionally depends only on the variable right before it in the sequence.

We exploit this assumption to translate an input sequence to another sequence using a Markov matrix or graph that models probabilistic transitions across variables. The graph consists of hidden states and observable variables in the structure below; note that this structure is similar to ⛓️ Markov Chain with observable variables tacked onto the original states.

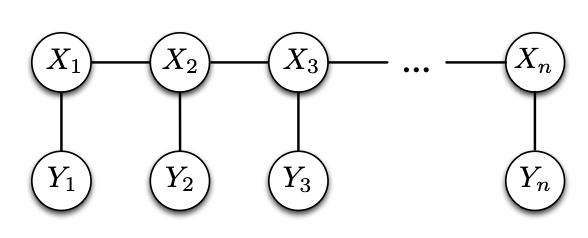
Each hidden state gives emissions with certain probabilities and transition to another hidden state with another set of probabilities. The input sequence we get is the observable variables , and for translation, our goal is to find the most probable sequence that generated these emissions.

To predict the probability of sequence given another sequence , we use 🪙 Bayes’ Theorem, ignoring the denominator and taking the highest probability.

For example, for speech recognition (predicting words from sounds), we start with a prior of the likelihood of each word along with likelihood of each sound given a word.

Forward-Backward Algorithm §

The forward-backward algorithm is an inference method for HMMs that estimates the hidden states given observations. Assuming is known, our goal is to compute .

To do this, we have the forward and backward steps, both computed using recursive message passing, similar to 🕍 Belief Propagation.

1. Forward step computes .
2. Backward step computes .

The forward and backward steps are detailed in the below sections. Assuming their values are known, we can then recover our target via marginalization over

due to the conditional independence structure of the HMM. Note that the first term in the product uses our backward pass, and the second term uses the forward pass.

Forward Pass §

For the forward pass, we want to compute ). The key observation is that we can marginalize over , then write a recursive definition:

Observe that the final term in our expression is exactly the distribution for . Thus, if we let our message

then we have

Our base message is , and we can pass this all the way to to get back our desired probability.

Backward Pass §

The backward pass is similar to the forward pass: our goal is to compute , and we’ll do so recursively with

Defining our message as

we have

with the base case (which we can derive from looking at the equation for ).