🤿 Gradient Blending

For image blending, we aim to put one object into another scene with a seamless transition. The key challenge is that if we simply copy and paste the object over, the area around our object won’t be seamless with the scene—making an obvious boundary.

One solution is to “soften” the boundary by using a soft alpha mask around our object when we extract and paste it onto the scene. While this eliminates the harsh transition, the result still looks off since there’s still a continuous change from background to object.

For best results, we use gradient blending. The key insight is that gradients contain the shape and texture information of our object, so we copy the gradient to the scene instead of the actual RGB values.

First, we blend the two gradient (magnitude and angle) maps using alpha blending, essentially creating a seamless edge image. From magnitude and angle, we can reconstruct the and gradients, and . Now, the problem is to build a picture from the two directional gradients such that

With just the gradient map, this problem has many solutions. We add a constraint using the boundary condition: RGB values around the object boundary (and outside) must be the same as the original scene. Now, we just need to compute the pixel values within the object mask.

We can frame our problem as a least squares optimization problem where the optimal solution satisfies the following:

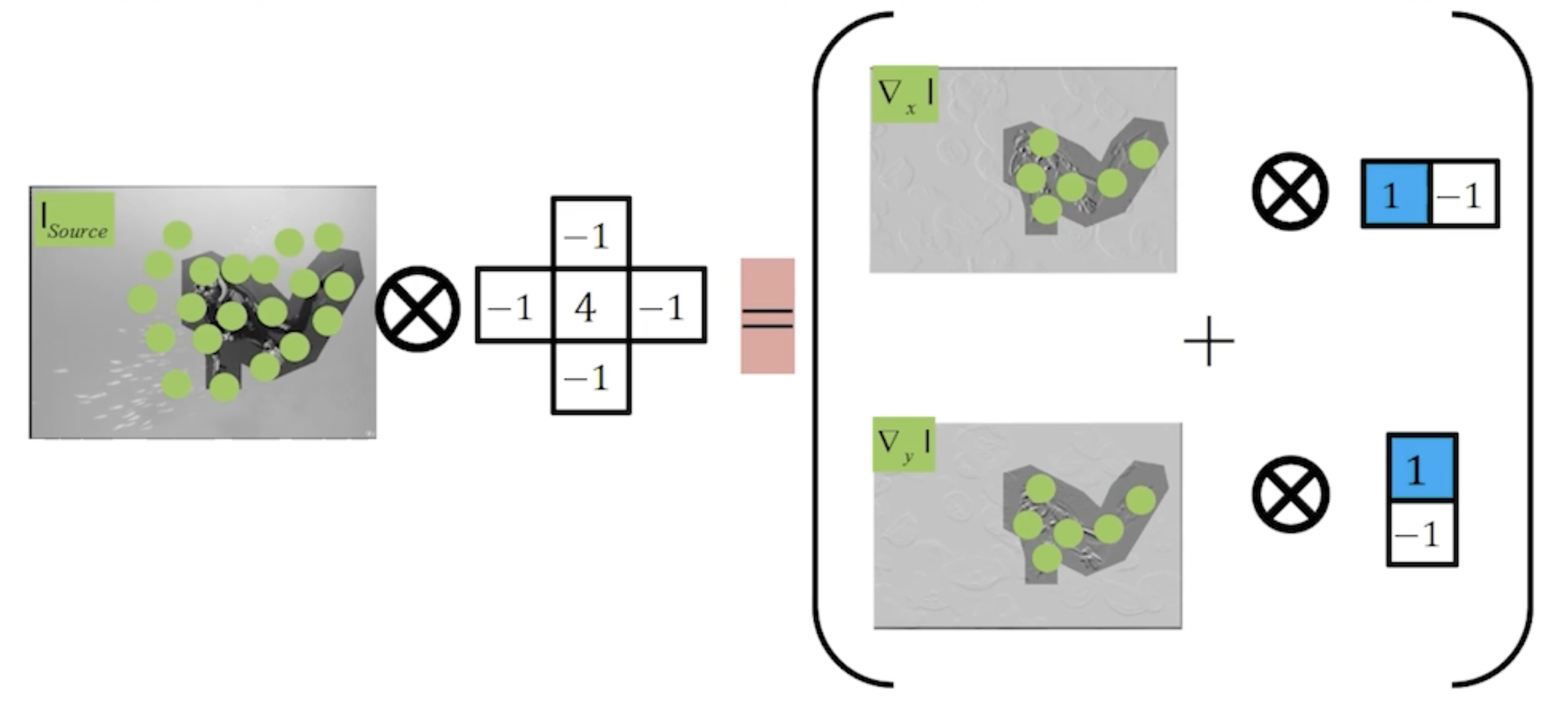
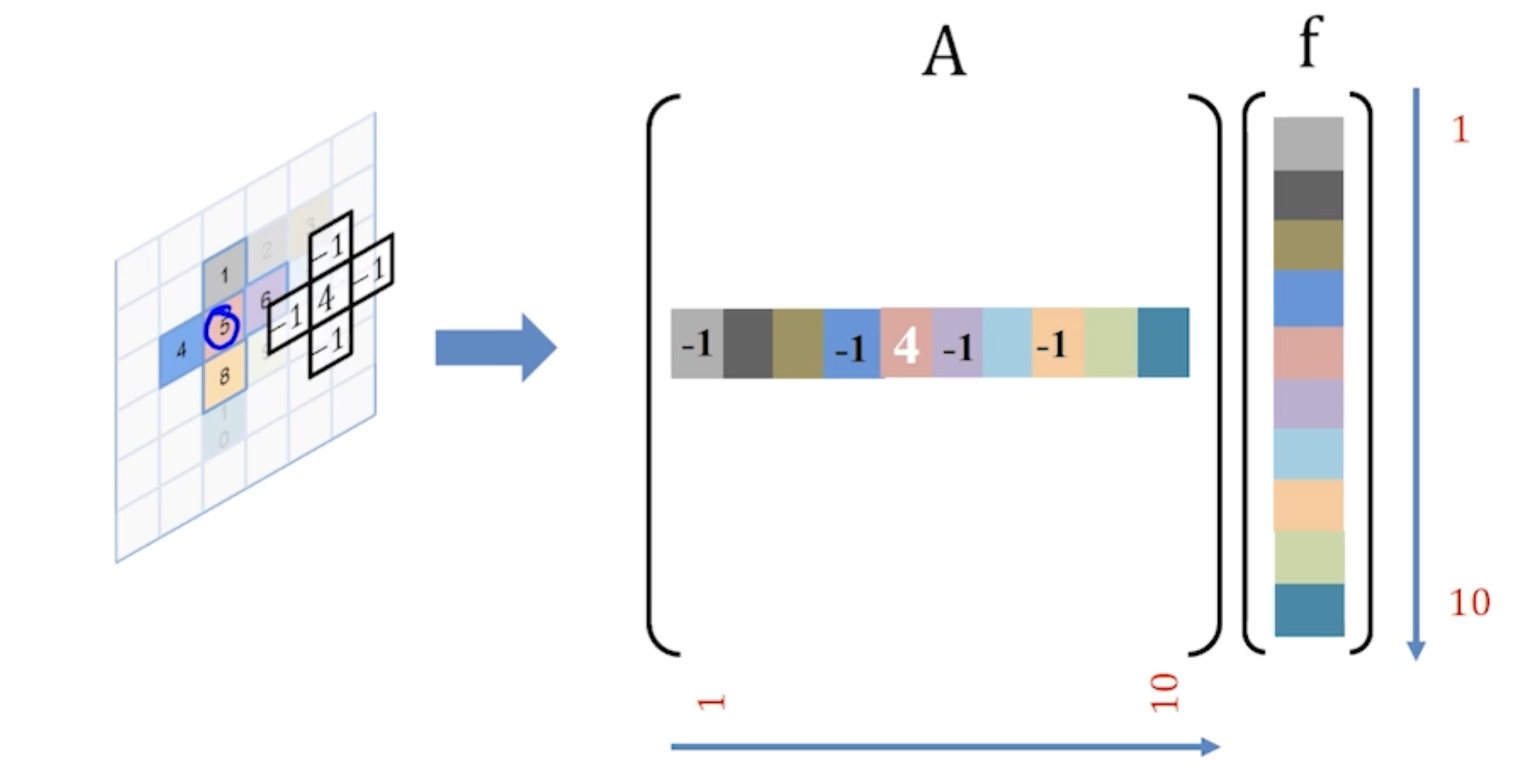
To solve this efficiently, we write down our equations in matrix form

First, we have a vector containing the laplacian of the original image (within our masked region). Next, we represent each pixel within our mask in the new image as a vector . Finally, we represent the laplacian operator as square matrix where each row applies the laplacian kernel to a specific pixel in .

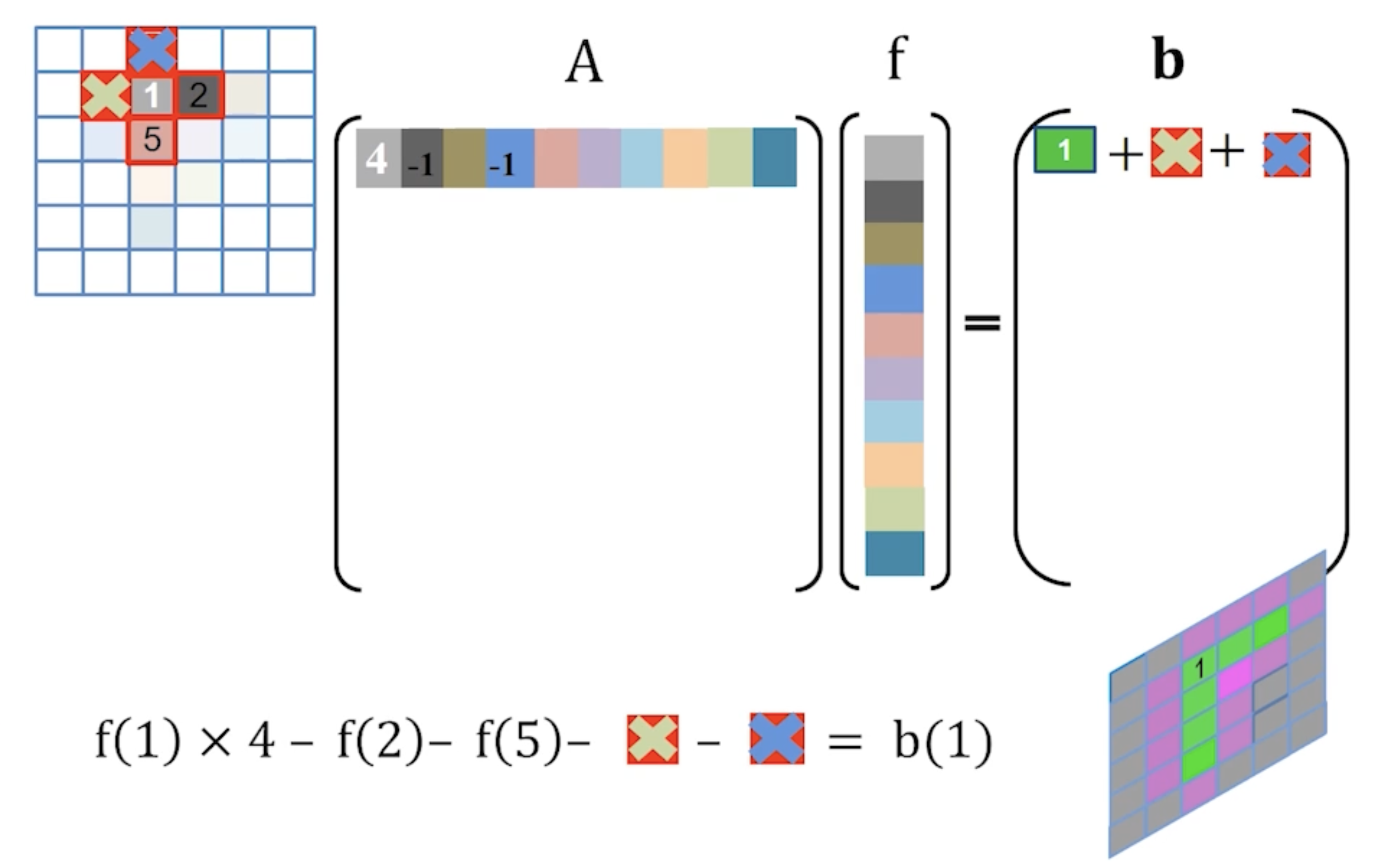
For pixels on the boundary, contains only for neighbors within the mask. The other pixels outside the mask are subject to the boundary condition, and we already know their values; we can move their constraint to the other side of the equation, to .

Now, we simply solve for and move the pixel values onto their respective positions in the final image.