👟 Unconstrained Optimization

Problem §

Given a convex objective and for parameters , a convex set, we want to find

Convexity §

A convex set is defined as a set where for all and ,

Intuitively, this is saying that the line between and is inside the set.

A convex function is defined as such that for and ,

In other words, the function is upwards curving. This is also known as 🌈 Jensen’s Inequality.

Moreover, if is convex and differentiable, then for all ,

This is illustrated below.

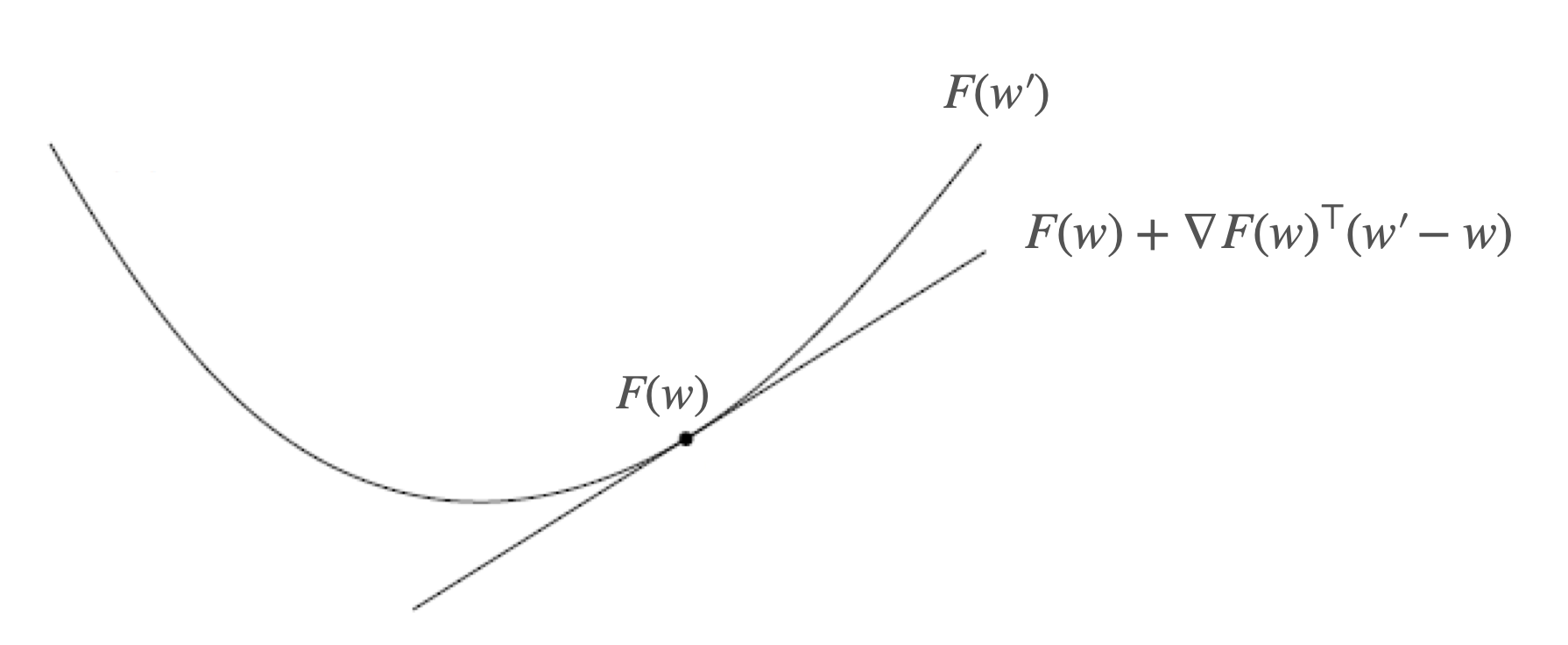
Lastly, for all , is a positive semidefinite matrix. This is also saying that the function always curves upwards.

Solution §

If is convex and differentiable, any that satisfies is a global minimum.

Convex Properties §

A convex function is -smooth if

A function is -strongly convex if

Gradient Descent §

These two properties essentially bound our function with and . We’ll use them to inform our algorithm below, called ⛰️ Gradient Descent.

1. Initialize .
2. For time steps,
   1. Update .

For a -smooth convex function , since we have an upper bound, we can minimize the quadratic

which gives us , our gradient descent step.

With this update rule setting , we will converge to optimal . Specifically, at time , we have

Also, if we let our acceptable error , we converge in steps.

---

Proof of Convergence

We’ll start with the smoothness property,

By our gradient descent step, we know , so rearranging for and plugging it into our equation above, we get

and simplifying, we have

Next, we use the convex property to get

and rearranging and plugging in the gradient update above,

Then, since

we let and and replace the above to get

Adding the inequality we derived above, we get

Finally, summing on both sides, we have the following:

where we also use the property that is non-increasing in the second step.

---

Moreover, if we also assume strong convexity with , we converge even faster, with

and convergence rate .