🍿 Two-View Stereopsis

Two-view stereopsis is the problem of finding per-pixel depth given two camera views and their relative pose ( and ). To do so, we need to match features across the two views and triangulate its position relative to the camera.

Disparity §

First, consider a basic setup where the cameras are facing the same direction and are related by a horizontal translation. That is, and . In this configuration, for a point in the world, and , and the only difference between the two photos is the x-coordinate of the pixel of a feature in the world. Using the Pinhole Model equation, we have

and the difference, called the disparity, is

Intuitively, this says that the farther the object is from the camera (higher ), the less disparity there will be in the two views. That is, close objects will be shifted more than farther objects, and we can use this equation to find if we first compute .

Stereo Rectification §

Before we continue to finding , we first note that any camera configuration can be “modified” to satisfy the setup above with and . Given any two views, if we project the image onto the plane parallel to the line between camera centers, we’ll get exactly this setup; this is the problem of stereo rectification.

Another way to view this transformation is to make the Epipolar Lines parallel; if this is done, then the epipoles are at infinity, thus making the image planes parallel.

Formally, our transformation will be a rotation , and we desire such a rotation so that for an epipole ,

The matrix that satisfies this constraint has its first row be exactly , then the other rows be orthogonal; that is, we have

such that

Thus, the steps of stereo rectification can be summarized as follows:

1. Estimate the Essential Matrix .
2. Compute the epipole by solving .
3. Build using the procedure above and also compute and from .
4. Let and .
5. Transform the left camera with and the right camera with .

Finding Correspondences §

Now, we will estimate . This is done by matching “windows” or image “patches” across the two views; patches with the highest similarity are deemed two views of the same point in the world, and disparity is calculated as the difference between patch centers.

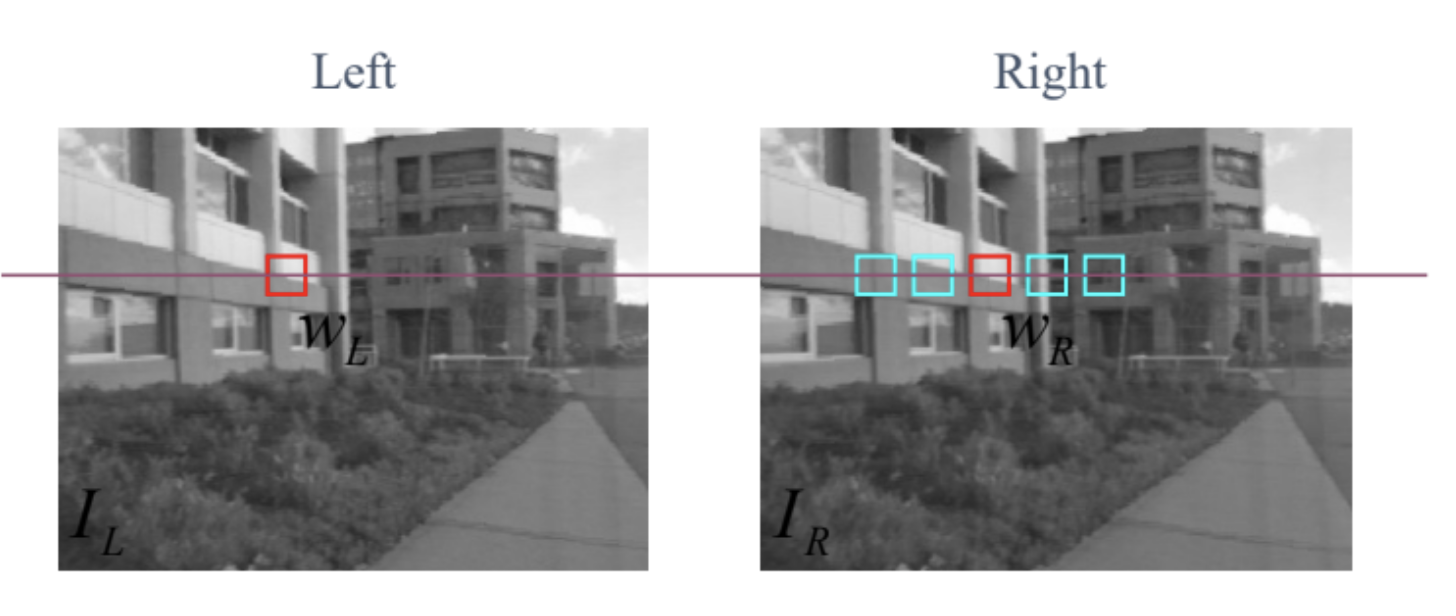
More specifically, for each patch in the left image, we’ll scan along the same coordinate in the right image to find the best patch (as measured by an similarity function, examples below). Then, for the corresponding patch in the right image, we’ll scan along the left image with the same procedure. If both sides output each other—left is most similar to right and vice versa—then we found a correspondence, and their disparity and depth can be computed.

There are multiple choices of similarity functions. For windows and , some examples are below:

1. Sum of squared differences (SSD):

2. Sum of absolute differences (SAD):

3. Zero-mean normalized cross correlation (ZNCC):

where and .

Photoconsistency §

Note that this stereopsis technique relies on two major assumptions:

1. There are few occlusions within the scene. Most features in the world are captured in both views.
2. The world’s surfaces is Lambertian; that is, it reflects the same color into both views (unlike mirrors or shiny surfaces).