🎧 NCSN

Noise conditional score networks (NCSNs) seek to approximate the true data distribution by learning the score function

of the distribution. 🎼 Score Matching is a natural way to train , and we can sample from it using ☄️ Langevin Dynamics.

However, because our data distribution is concentrated around manifolds in the full data space (as per the 🪐 Manifold Hypothesis), our model doesn’t learn accurate scores for the rest of the image space, preventing convergence and mixing between modes. A visualization is below.

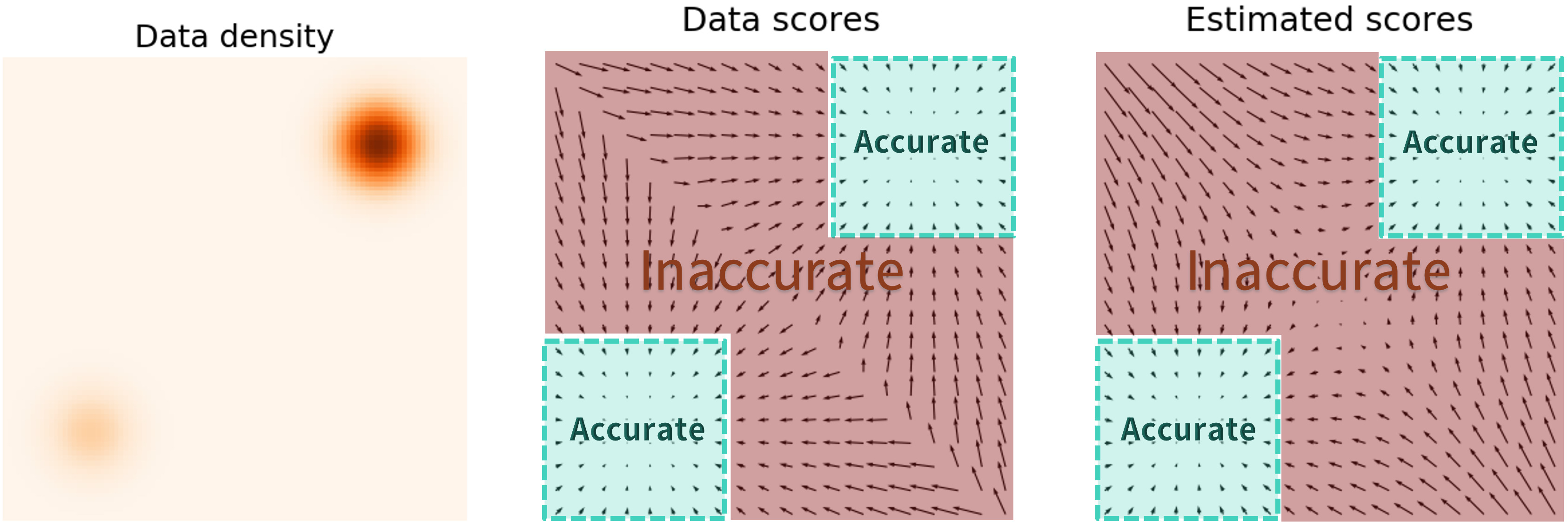
The solution is to perturb the data distribution with multiple levels of noise, which populates the low-density regions and allows our model to learn scores from them. Specifically, we set noise scales and define

as our noisy distribution for each scale. Our score model is now conditioned on the scale as well, so we have

We can still train using a weighted sum of Fisher divergences

where is a weighing function set as to balance the score matching loss for different variances.

To sample, we use annealed Langevin dynamics, which essentially performs Langevin dynamics for steps for each noise scale, starting from and going to . In doing so, our randomly initialized sample will be able to use the score of the extremely noisy and move toward the manifold.