📌 Laplace Mechanism

The laplace mechanism is a differentially private algorithm for computing statistics over a dataset. The key idea is to add laplace noise to the true statistic, thus incorporating randomization and ensuring privacy.

Formally, the mechanism takes dataset (where person ’s data is ) and computes some function

Our algorithm first computes exactly, then outputs where is noise sampled from the laplace distribution.

Sensitivity §

To formally specify the degree of noise and its relation to the definition of differential privacy, we define a measure called “sensitivity.” Intuitively, sensitivity is the magnitude of change between two neighboring inputs; that is,

for neighbors and .

Some common sensitivity examples are below:

1. Average: for and .
2. Standard deviation: for the same .
3. Maximum: for the same .
4. Median: for odd , split in the middle.

Laplace Sampling §

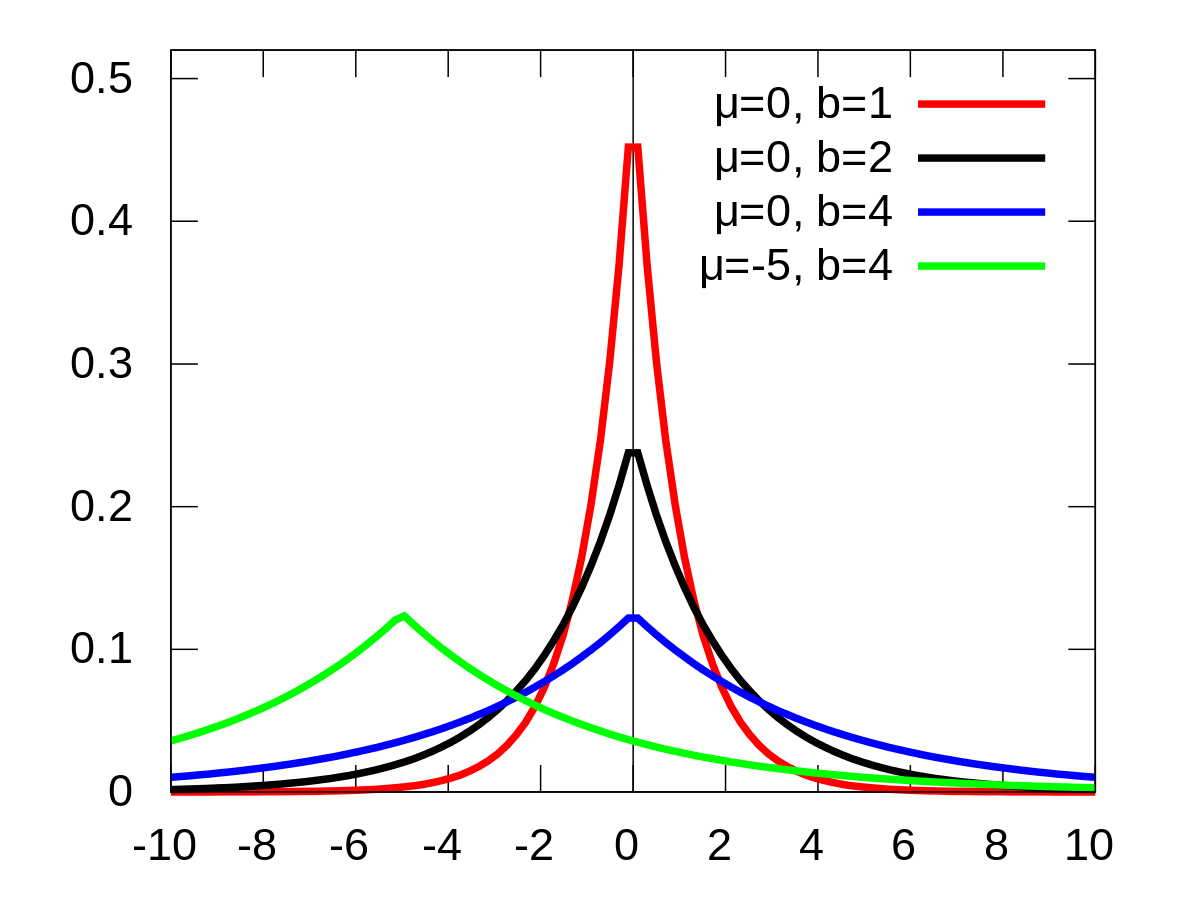
For a laplace distribution centered at with variance , we randomly sample a value with probability

controls the magnitude of noise we add to , so in the laplace mechanism, we set with the desired degree of differential privacy via the equation

Note that this formulation is extremely useful if our sensitivity is inversely proportional to the number of samples . This mechanism can be used for any function such that as , and thus .

Differential Privacy Analysis §

We’ll now show that the algorithm above is -differentially private. Let be neighboring inputs with laplace mechanism distributions . For an output value , we have

Now, observe that is the difference from and to some value ; this difference is bounded by the case when and are on different sides of (one higher, one lower); that is,

Thus, our equation above is

Note that the above derivation showed the difference in probabilities for neighboring individual outcomes. To relate this to the definition of differential privacy, which is concerned with all possible sets of (disjoint) outcomes, we have

Thus, our laplace mechanism is -differentially private.