Group Equivariant CNNs (G-CNNs) generalized the standard 👁️ Convolutional Neural Networks’ translation 🪞 Equivariance to other symmetries, specifically rotation and reflection.
Symmetric Groups
A symmetry of an object is a transformation that leaves it invariant. The set of symmetric transformations is a symmetry group.
The translation, rotation, and reflection operations are all symmetries for our feature map. Thus, they form the p4m group parameterized by
This matrix is applied to Homogenous Coordinates for the transformed pixels. That is, a member of the group
Group Functions
However, observe a transformation on a pixel is equivalent to the inverse transformation on the image; for example, moving a pixel to the left in
Intuitively, this is saying that the value at point
A feature map in p4m space and the operations a group can perform on it is below.
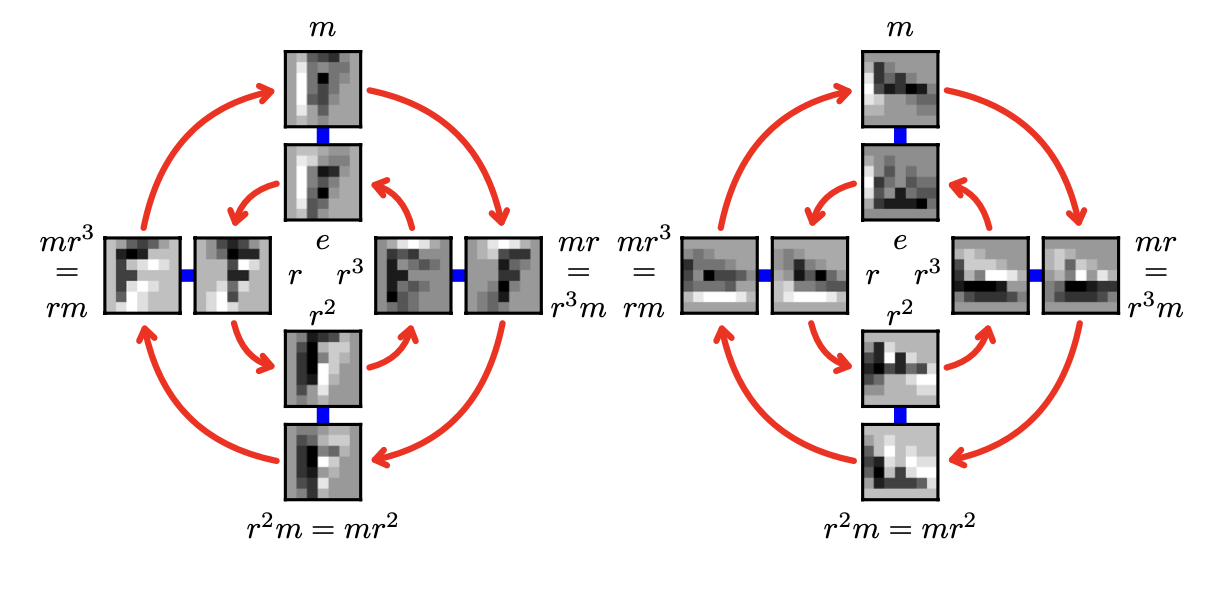
G-Convolutions
Now, we can generalize standard convolutions to groups. Note that the original convolution is CNNs is performed on a group consisting of translations; for a filter
for each offset
The key insight here is that
Thus, instead of thinking about
Therefore, we can generalize to any symmetric group
This is the G-convolution that acts on the input feature map.
However, since this results in a feature map
Pooling layers can be defined using the same idea, and nonlinearities are still performed over each value,