♻️ Convolution

The convolution of two functions and is a function that applies the domains of and onto each over through multiplication. Formally,

Intuitively, this is a fancy multiplication operation on two functions that flips the domain of (thereby making ) and offsetting it by .

In computer vision, convolutions are generally applied in 2D over 🏞️ Images. If we let be our convolution kernel and be our image, the convolution operation computes a new image where the value at a single pixel is

By flipping the kernel, convolutions are associative, commutative, and distributive. They also preserve linear independence, .

Impulse Function §

The impulse function is a 2D array where one index is and others are . Convolutions with impulse functions reveal some nice properties:

1. For an impulse function with in the middle, .
2. For impulse functions with in a certain direction, shifts towards that direction.

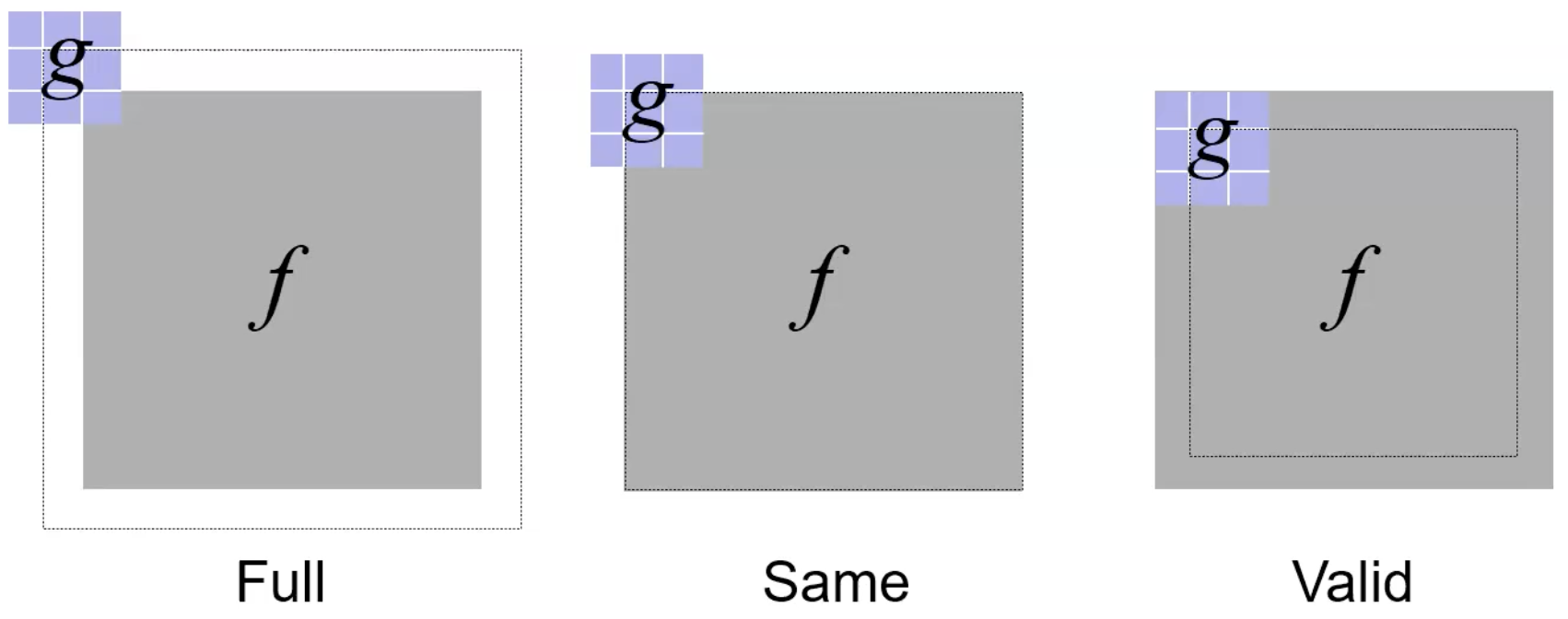
Padding §

If we apply an filter with only on pixels in our image, our result will have smaller dimensions. To preserve the same size—or even potentially expand the size—we can use padding: we add a border around our original image, thus enlarging it before applying the kernel.

There are three common padding methods: full maximizes the dimensions, same preserves the same dimensions, and valid shrinks dimensions (and uses no padding).

Filtering §

A very similar idea is filtering, which performs the same operation as a convolution without flipping . Thus, we can think of it as computing a weighted sum of values in using as the weights.

Note that in 👁️ Convolutional Neural Networks and most machine learning systems, we actually use learned filters instead of convolutions. The reason is that since the values are learned anyways, there’s no difference between flipping .