🚨 Bayesian Network

Abstract

Bayesian networks are graphical models that capture the conditional independences and dependences between random variables of a probability distribution. Specifically, each directed arrow specifies a direct conditional dependence between its two nodes.

Bayesian (or belief) networks represent conditional independence and dependence assertions over a complex joint distribution via a directed acyclic graph.

1. Each node is a random variable that has conditional distribution . We can think of this conditional as represented by probability tables.
2. Each directed edge is an conditional dependence assertion.

The following is an illustration of a simple network.

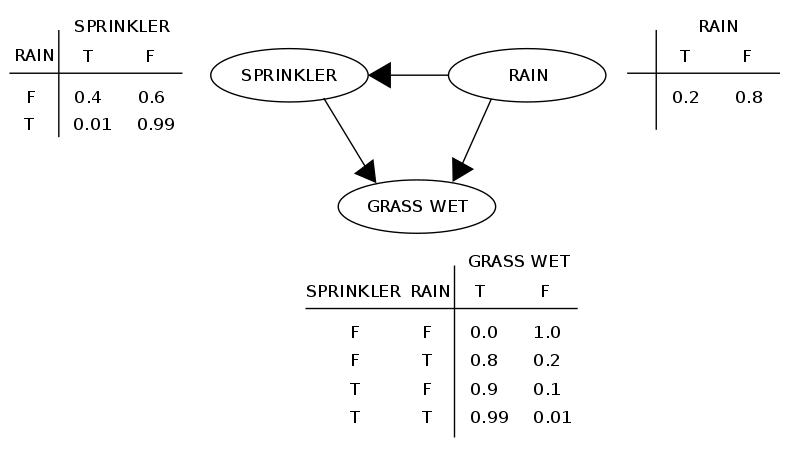
By representing conditional dependences using arrows, our graph captures both the conditional independences and dependences of the probability distribution. As a simple example, if we have a simple graph with two nodes and , an arrow from to means that depends on whereas the absence of an arrow means that and are independent.

One variant, called ⏰ Dynamic Bayesian Networks, uses these variables to capture changes over time with the Markov assumption and time invariance.

Independencies §

In more complex graphs, we can interpret the directed edges as follows.

1. With , we have but . The former is because knowing anything more about wouldn’t help us learn more about since affects but we know already. As for the latter, if we didn’t know , learning gives us information about and thus also about .
2. With , we have but . This follows a similar reasoning as the previous example: knowing blocks the flow of information from to since our knowledge of would be redundant given , but not knowing allows the information to flow.
3. With , we have but . The former is because knowing gives information about unknown , but more information about does not reveal anything about . On the other hand, if we did know , since both and affect , knowing would reveal some information about .

A common example for the third configuration is the alarm scenario: is a burglar, is an earthquake, and is an alarm. If we know the alarm went off, we would wonder whether it was caused by a burglar or earthquake. If we also knew that there was a burglar , then an earthquake would seem more unlikely. Similarly, if we knew there was an earthquake, a burglary is also less likely.

Active Trails §

Active trails represent flow of information; variables connected by an active trail are not conditionally independent. For each triplet in the trail, one of the following must be true.

1. , not observed.
2. , not observed.
3. , not observed.
4. , observed or one of its descendants is observed.

D-Separation §

If there is no active trail between and given a set of observed variables , they are conditionally independent and are d-separated. One immediate conclusion is the local Markov assumption, which states that any node is d-separated from its non-descendants given its parents.

Note

All d-separated independences in the graph are independencies in the probability distribution, but it’s not guaranteed that all independences in the distribution are represented in the graph.

I-Maps §

Let be the set of independencies that hold in distribution , and let contain all d-separated pairs . We say that a distribution factorizes over if it can be factorized over . That is,

This is the case when , and we call an I-map (independency map). Conversely, if is an I-map for , then factorizes over .

Note that we don’t require to perfectly enforce all independences in . Rather, we only require that the conditional independencies in are also in . Thus, as an example, a fully-connected network is an I-map for any distribution since there are no independences, .

Some graphs can also encode the same independences—we call them I-equivalent. By the independencies specified above, two graphs are I-equivalent if they have the same skeleton (same edges, not considering directionality) and same v-structures.

Info

A more connected network represents a distribution with few conditional independences. Each conditional independence limits the size of the class of distributions that satisfy it, so a more connected network models a larger class of joint probability distributions.

Ancestral Sampling §

To sample from our distribution, we can go through the nodes from top to bottom. Specifically, we first topologically sort our variables, then go in order, sampling from each table. The sorting guarantees that we calculate all the conditionals in order.