🌈 Jensen's Inequality

For random variable , if is a convex function, we have

In other words, applying the function to the expectation after gives us a smaller value than applying it first. If we apply this to two possible values and with weights and , we can view it as the difference between the middle point on the pink versus black lines. The pink represents applying the average after , and the black represents finding the average before.

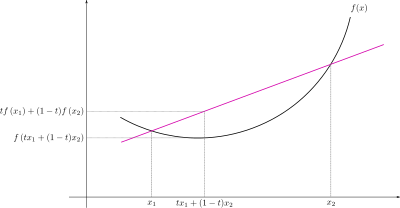
Jensen’s inequality works for concave functions too, with the inequality sign flipped:

This inequality is commonly used with the logarithm, giving us