🥢 Generalized Linear Model

Theory §

Generalized Linear Models generalize linear regression to non-linear data by either transforming the output with a link function or input with basis functions.

1. With link function , our prediction . This link is derived by associating with a certain exponential family distribution, chosen depending on the type of output we expect.
2. With basis functions , our prediction where . This usually works well with gaussian basis functions instead of polynomial functions.

Exponential Family §

The exponential family of distributions is defined by the form

where is the natural or canonical parameter, is the sufficient statistic, and is the log partition function.

Distributions that fall into this family include the following.

1. Bernoulli: where , , , and .
2. Gaussian (for simplicity, let ): where , , , and .
3. Multinomial, Poisson, Gamma, Exponential, Beta, and Dirichlet.

Another way we can view the link function is that it predicts the expected value of the distribution we select, with . We choose the distribution depending on our problem: Bernoulli for classification, Gaussian for regression, and the others depending on other output requirements.

Radial Basis Functions §

Radial basis functions are especially powerful and common. They use gaussian 🍿 Kernels, is ’s position on kernel ’s distribution, or . These kernel centers are calculated with 🎒 K-Means Clustering, chosen randomly from datapoints, or estimated with nonlinear regression.

By projecting our data onto the multiple RBFs, we can perform changes to our data.

1. If , we essentially perform dimensionality reduction. Conversely, with , we increase dimensionality.
2. With , we switch to dual representation that relies on pairwise relationships between our datapoints.

The following is an example of two gaussian kernels for binary classification. (This is technically a Gaussian Discriminant Analysis model, but the idea is similar.)

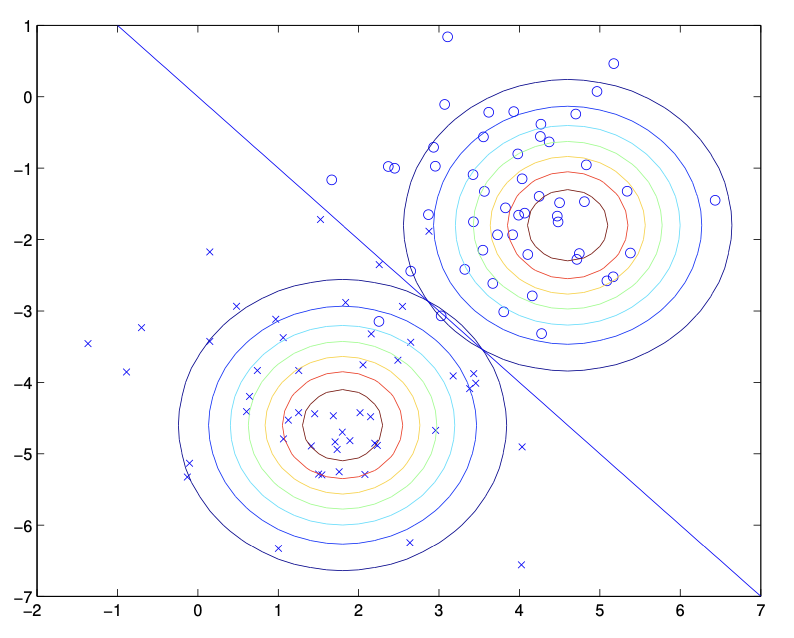
Using GLMs, we use the same idea of applying weights to features but get more versatile results. Specifically, a GLM is a model that fits any that follows an exponential family of distributions; this includes Gaussian (linear regression) and Bernoulli (logistic regression).

Model §

Our model’s the same as linear regression with the link or basis function additions. We still optimize the weights , potentially with regularization, and select or beforehand.