🧨 Score SDE

The score SDE, a time-dependent score-based model, seeks to learn the score of the data distribution. This is an extension of the 🎧 NCSN into infinitesimally small noise-scale steps. This model also shares heavy resemblances to 🕯️ Diffusion Probabilistic Models.

SDE Perturbation §

Let be the data distribution perturbed with noise at time . Unlike the discrete noise scales in NCSN, follows a stochastic differential equation

where is white noise. At , , the original data distribution, and with for high enough , , a tractable prior noise distribution.

As increases, we increasingly add noise, defined by diffusion coefficient , and guide the general direction with , the drift coefficient. and are hand-designed.

SDE Reversal §

To recover our data distribution from , we reverse the SDE using

The time-dependent score-based model seeks to learn this score,

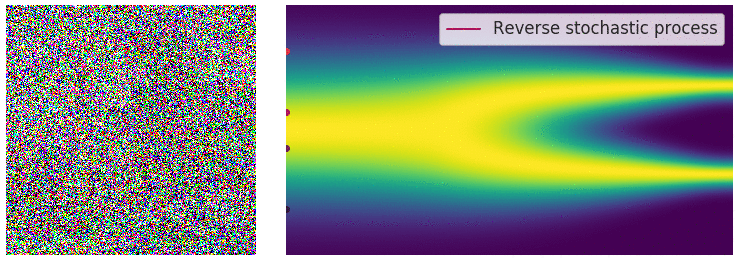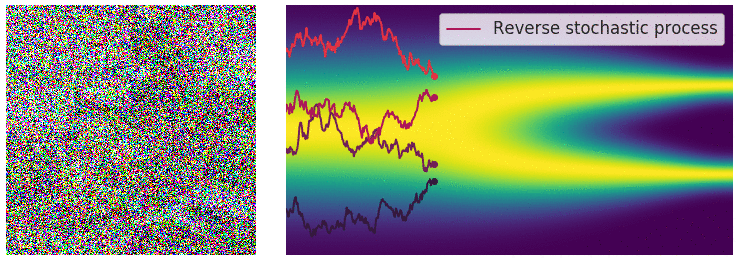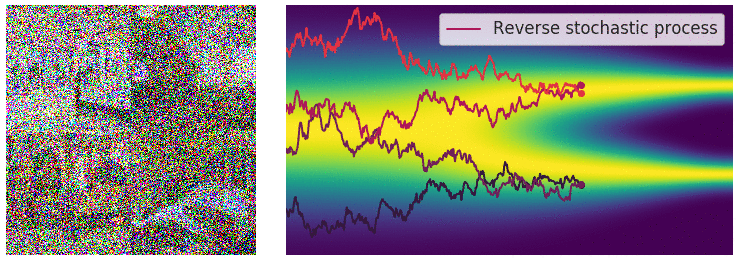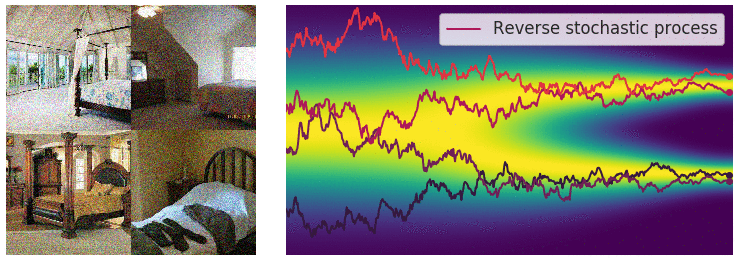
Optimization §

We follow a similar setup from NCSN, training on the objective

with typically set to the inverse of the expectation to balance losses over time.

Predictor-Corrector §

To computationally solve the reverse SDE, we can use the Euler-Maruyama method, which quantizes time and defines to get the following:

This can be improved via fine-tuning with 🎯 Markov Chain Monte Carlo. The predictor is a SDE solver like Euler-Maruyama that predicts the next step , and the corrector uses MCMC methods like ☄️ Langevin Dynamics to improve the sample using the score . In other words, the predictor moves us to the next data distribution , and the corrector finds a better quality sample from .

With this method, we can achieve incredibly realistic samples from our modeled distribution.

Probability Flow ODE §

One limitation of the SDE method is that we can’t compute the log likelihood of our model. Fortunately, we can convert the SDE to an ordinary differential equation

This resembles a 🎱 Neural ODE, which thus allows us to compute the exact log likelihood.