🕰️ Autoregressive Model

Autoregressive models parameterize the joint distribution by breaking it down into conditionals for each dimension . We have

is the random variables with index less than .

Info

The “autoregressive” name comes from time-series models that predict outcomes based on past observations. In this setting, is analogous to the th time step.

If we parameterize as a table, the number of parameters we need grows exponentially with the number of dimensions in . To make computations practical, autoregressive models use a fixed number of parameters to map to the mean of the conditional distribution, which we typically assume to be Bernoulli. Thus, we have

where are the parameters that specify , the mean function. Note that the standard formulation allows separate parameters and functions for each dimension .

Info

For non-binary discrete or continuous random variables, we can predict softmax for the former and parameterized distributions (mixture of Gaussians, for example) for the latter.

Since we restricted our function to a fixed number of parameters, we’re limiting the expressiveness of our model. This is the tradeoff we get using this computationally-feasible representation.

Variants §

FVSBN §

If we let our function we a linear combination of the inputs with a non-linearity,

with , we get the fully-visible sigmoid belief network (FVSBN), a specific structure of the general 🕋 Deep Belief Network.

To increase the expressiveness, we can simply add more hidden layers and use a 🕸️ Multilayer Perceptron for our function instead.

NADE §

Neural autoregressive density estimator (NADE) is an alternative method that shares some MLP parameters across conditionals, so we have the following:

The first layer of computations uses shared weights, and the second uses separate weights. This reduces the total number of parameters to and allows for more efficient hidden unit activations.

MADE §

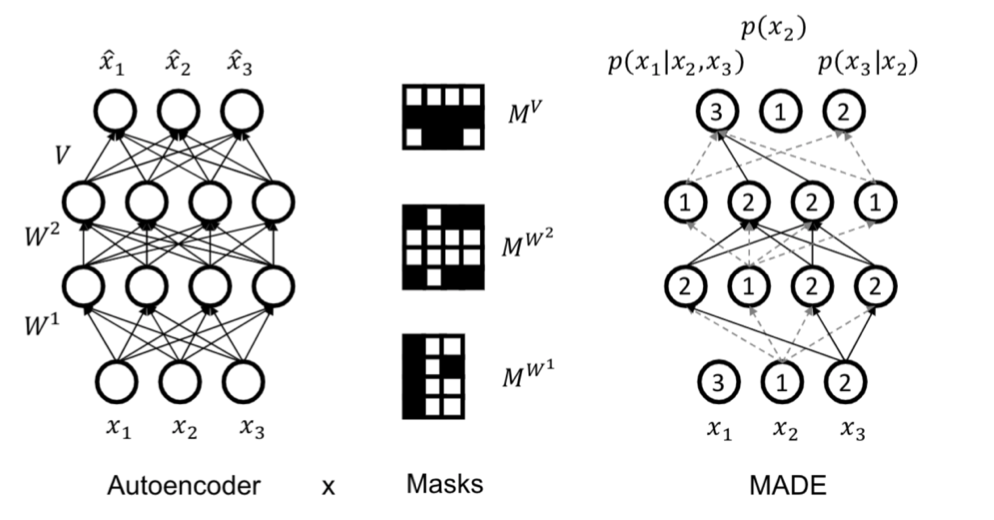
Masked autoencoder for distribution estimation (MADE) combines the autoregressive property with an 🧬 Autoencoder, which aims to reconstruct our input from the sampled .

However, by the autoregressive property, a standard architecture doesn’t work because all outputs require all inputs. MADE sets a certain order for the input dimensions and masks out certain paths in the autoencoder to enforce the autoregressive property; that is, in MADE, isn’t conditional on any input, is only conditioned on , and so on.

Recurrence §

To model , most methods apply more weights as increases. An alternative approach is to use 💬 Recurrent Neural Networks to evaluate the “history” one-by-one. We thus maintain a hidden layer “summary” of the past inputs and use it to output parameters for our conditional:

Optimization §

Autoregressive models benefit from explicitly modeling , so we can directly optimize it via ✂️ KL Divergence,

Since is constant with respect to , this objective is equivalent to

With an analytical form for , we can directly use 🤔 Monte Carlo Sampling, so now we want

where is our dataset of samples from . In implementation, this is a loss function that we can optimize via ⛰️ Gradient Descent.

Sampling §

To sample from our learned distribution , we first sample , then , and so on to build .