🎲 RANSAC

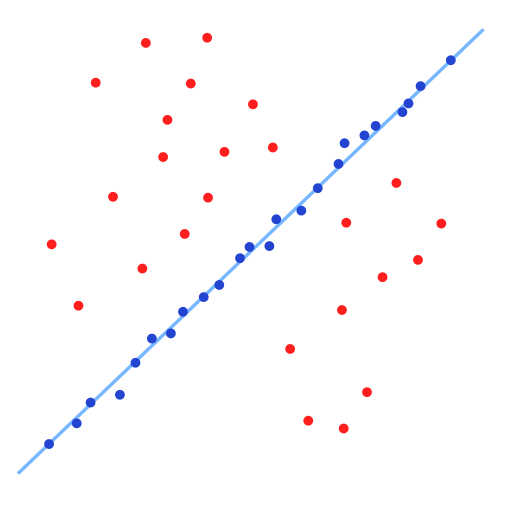
Random Sample Consensus (RANSAC) is a method for fitting a model to data that contains potentially-harmful outliers. In this sense, RANSAC can also be thought of as an outlier-filtering algorithm that estimates model parameters after removing outliers.

Define the “minimal sample set” as the smallest set of datapoints we need to define a model. The RANSAC algorithm essentially fits a bunch of minimal sample sets selected at random and chooses the best one.

More specifically, the algorithm repeats the following for iterations:

1. Randomly choose the minimal sample set of datapoints.
2. Fit a model to this set.
3. Check each datapoint’s error in this model via some pre-defined error measure, and count the number of errors that fall outside a certain threshold—these points are outliers.

At the end, choose the model that has the fewest outliers. Alternatively, we can stop the loop when we fall within a certain number of outliers.

Though this algorithm doesn’t deterministically guarantee the best model, we have some probabilistic guarantees due to randomization. If is the probability of choosing a true inlier, the probability of choosing an all-inlier minimal sample set is . Then, the probability of failing to find a model fit on this set is , giving us a probability of success of

Linear Regression §

In the most simple case, RANSAC can be used for linear regression. Our minimal sample set consists of two points, which define a line. The algorithm then tries many possible lines, and if there are enough inliers, we’ll eventually randomly choose two inliers and get the desired linear model.