💦 Optical Flow

Optical flow finds the visual flow in videos, sort of like 🍿 Two-View Stereopsis but with small baselines. Formally, we wish to compute the positional and angular velocities of the camera, and .

Local Search §

Since the frames of a video are extremely similar, we expect image patches to move very slightly in adjacent frames. Let two adjacent frames be and ; the local search algorithm simply searches for matching pixels in a nearby area, finding the one with most similar intensities:

where is a point on the image and is the displacement.

Though this does work in practice, its main weakness is that to search, we discretize and cannot recover an extremely-accurate flow.

Optimization §

Rather than performing an exhaustive search, we can instead frame optical flow as an optimization problem where we want to minimize

The optimal is at a minima of this function, so its derivative must be zero. Thus, we have

Since a variation with for is equivalent to a variation in , we can rewrite the fraction, giving us

and revealing that the fraction is exactly the image gradient of . Now, we need to solve for , but is an image and thus a nonlinear function of the pixel locations, making this equation difficult.

Taylor Approximation §

To simplify our task, we can approximate with a 🎤 Taylor Series,

Visually, this is assuming that the shifted image is the sum of an unshifted version with its gradient, which “shaves” off edges.

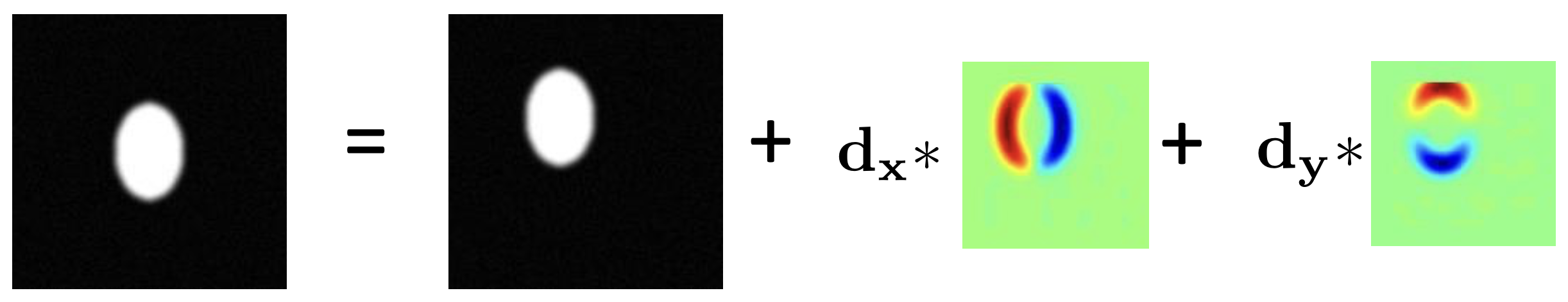
Now, our original optimization task turns into

In this form, our problem looks very similar to the least squares problem,

Indeed, we can plug our approximation back into our optimization equation, arriving at

and reordering, we have

exactly mirroring the least squares solution .

Another common form of this equation is

The coefficient on the left is the second moment matrix that describes, for each pixel, the second-order gradients. The term on the right is the difference between images, then multiplied with the second image’s gradient. We can compute both terms, and thus we can find .

Gradient Descent §

However, since we used a Taylor approximation, our first solution for might not be perfect. We can refine our result applying the displacement to , then recompute everything again, apply it again, then recompute, and so on. Each iteration will decrease the error, and our final result is the cumulative displacement.

Windows §

Finally, one more thing to note is that we usually perform this optimization over small patches (windows) of an image rather than individual pixels. This objective is

where is our window. With our Taylor approximation, we can absorb the sum into matrix form,

and again apply the least squares solution ; simplifying, we find

(Note that here denotes a point, as in . Sorry for the odd notation.)

Large Displacements §

Our gradient operator only covers the gradient of our second image. If the difference between images is too big, the gradient operator will not capture the first image, , which makes the least-squares problem unsolvable.

The most direct solution is to use a larger gradient kernel, allowing information to propagate across more pixels and hopefully incorporating parts of the first image. Alternatively, we can use the gaussian pyramid (from 🔺 Image Pyramid) and perform optical flow on smaller images, thereby making the same kernel larger relative to the image.

Texture Challenges §

Our approach relies on the assumption that brightness stays similar and the absence of occlusions. We also need the patch to be sufficiently interesting for the left product to be invertible. As such, there are certain scenarios where this algorithm doesn’t work well:

1. “White wall” problem: in the absence of texture, we get no gradient and thus no flow.
2. “Barber poll” problem: with one-dimensional texture, we get a constant gradient and insufficient information to compute the true flow. This is why the barber pole has an illusion of moving up or down when it’s actually just rotating.

Recovering Velocities §

Nevertheless, in the case where we do get , we can find velocities . First, consider a static point in the world. When we move our camera, its projection moves in the image plane with ; however, doesn’t actually move in the world.

Let be the point in world coordinates and be the same point in camera coordinates. We have the following derivation:

Since can’t be zero, the quantity inside the parenthesis must be equal to zero. This equality gives us the scene flow equation

To relate this to calibrated coordinates, we can differentiate the projection equation,

Finally, combining the two equations above allows us to relate the change in calibrated coordinates with and ,

The first term is the translational flow, and the second is the rotational flow that’s independent of depth.

If is known, we can solve this equation of 6 unknowns with 6 equations (3 flow vectors). If is unknown, we have the following two methods.

Pure Translation §

In the case of pure translation, we have the translational flow

and the condition

which says that the image point, flow, and linear velocity lie on the same plane. We can then solve for from multiple by solving the homogeneous system

via SVD to find the nullspace.

General Case §

In the general case where both and are unknown, we’ll use the above combined equation

where

Rearranging, we have

and for points we have

Our guess for determines the right hand side; if we have , we can then solve for the rightmost vector with the pseudo-inverse . Thus, plugging this in for the rightmost vector, we can then find the that optimizes

and then recover both and .

Time to Collision §

One useful thing we can do with optical flow vectors is estimating the time to collision of the camera with something in front of it. Observe that the translational flow

all intersect at a single point—the focus of expansion (FOE). This point can be computed as

The time to collision (TTC) can then be measured as