🖌️ Image Morphing

Image morphing finds the “average” between two objects. We’re not simply averaging the the two object images; rather, we’re also warping them to fit the same shape.

Warping §

First, we need to spatially align parts of the image. To do so, we need some external information on what corresponds with what. Specifically, we have a human label point correspondences—for example, where eyes are in each image.

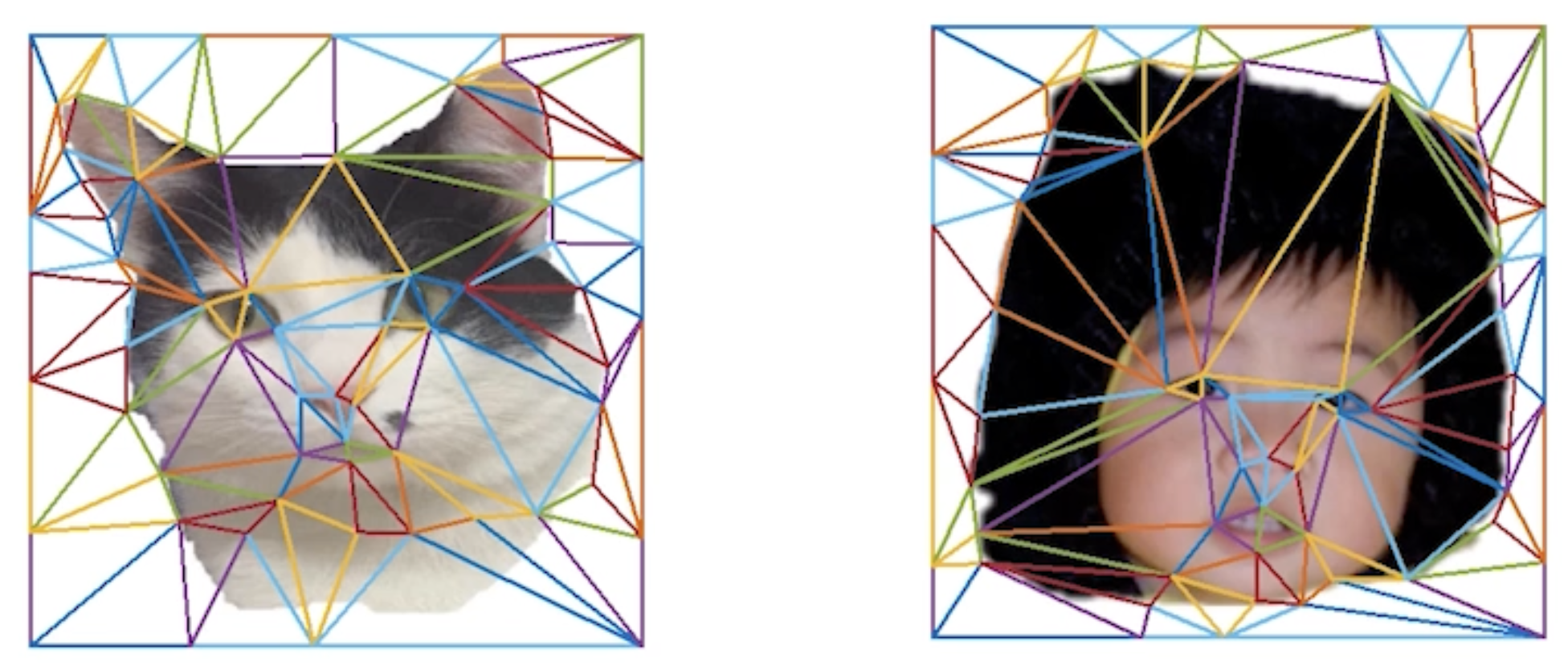
Delaunay Triangulation §

Given these points, we’ll construct a triangular mesh over the image using Delaunay triangulation: we construct a Voronoi diagram that splits the image into per-point cells where each pixel is assigned to the cell of the closest point; we then connect any two points that share a cell edge. This is guaranteed to give us the “best” possible triangulation, avoiding oddly shaped or skinny triangles.

To make sure our triangles are consistent across the two images, we compute an “average” image by interpolating each point correspondence and perform triangulation on this. We can then use the same triangulation for both images, thereby giving us triangle correspondences.

Affine Transformation with Barycentric Coordinates §

Now, we need to transform these triangles according to . We can interpolate the points via , thereby giving the triangle locations. To warp the pixels within each triangle, we calculate each pixel’s Barycentric coordinates, which are relative to the three points of the triangle; thus, the pixel will move along with the triangle vertices during our transformation.

Given vertices , we write Barycentric coordinates as

In other words, is a weighted combination of the three vertices.

Rewriting the equation above, we can view and as our movement, starting from , along the vectors and :

Another interpretation is that is the (inverse) distance to along the direction perpendicular to its opposing edge (and similarly for and ).

To solve for , we can solve a linear equation using known and ,

Now, when we move our triangle’s , we keep constant and can use the same equation to calculate new positions for our pixel.

One important detail is that with forward warping, there might be parts of our resulting triangle that aren’t warped onto, thereby creating holes. Instead, we should perform backward warping for each pixel in our target image, then get the color via interpolation within the source image.

Cross Dissolve §

Now, with the positions calculated, all we need to do is blend the color. We do this with cross dissolve, which takes an average over a time interval ,