🔺 Image Pyramid

🏞️ Images contain information at multiple scales. To decompose them, we can construct an image pyramid: representing it as sized images.

Reduction §

First, given an image, we want to reduce its dimensions by half. A naive sub-sampling solution might be to take every other row and column, but this is susceptible to aliasing (distortion). To get around this, we first blur the image via a convolution with the Gaussian filter (see 🍿 Gaussian Kernels); then, subsampling every other row and column produces smoother results.

Specifically, we use a filter of size . For illustration, will be one-dimensional.

1. The center, .
2. The values around it, .
3. The edges, .

For , we get an approximated gaussian distribution. However, most applications empirically use .

Expansion §

Given a reduced image, we’re also interested in expanding it back out. To do this, we first double the dimensions by adding -filled columns and rows between each image column and row (this is analogous to the reversal of sub-sampling). Then, we apply another convolution kernel, filling in the missing information using information from the neighboring pixels.

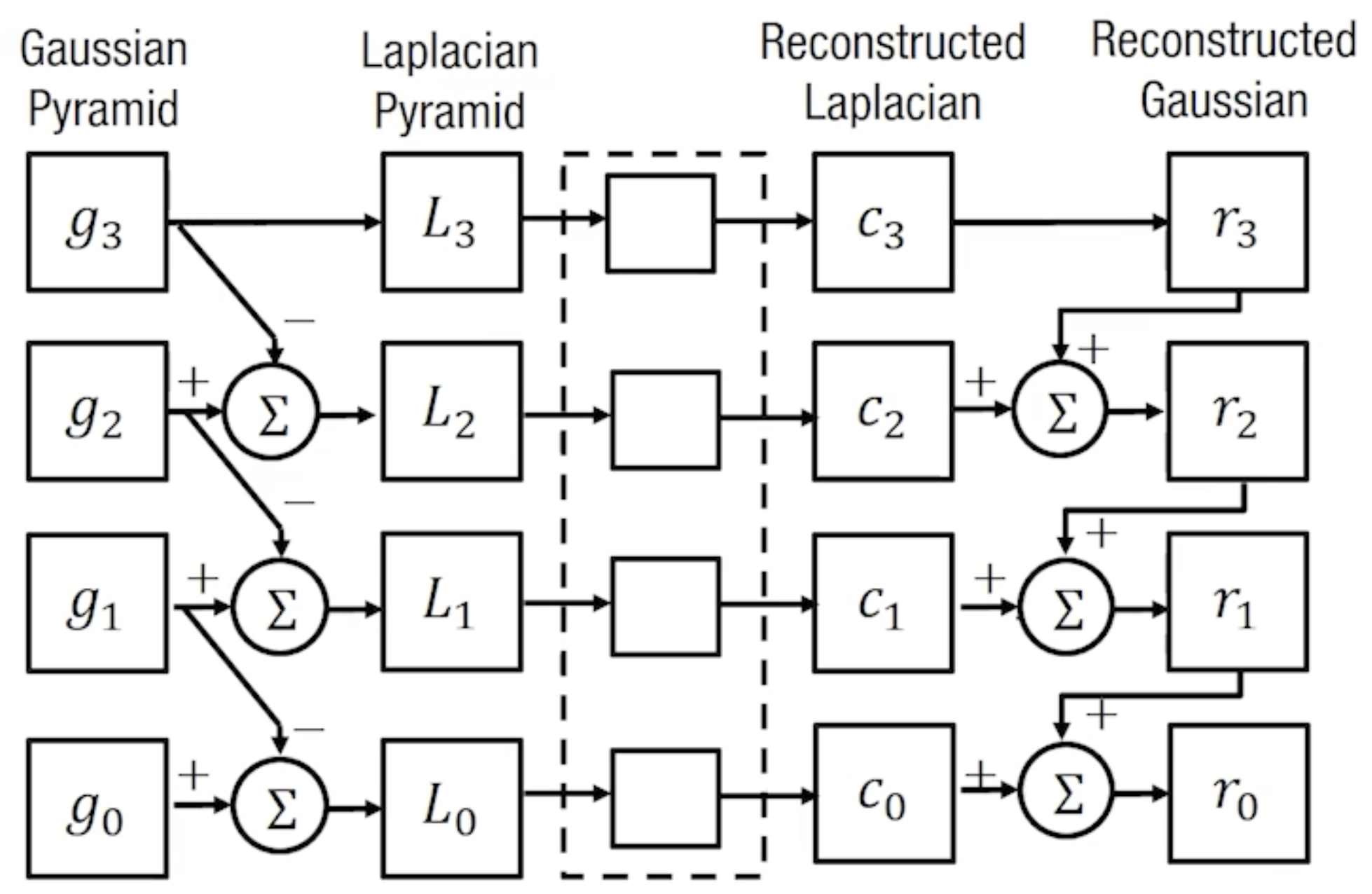
Gaussian Pyramid §

The gaussian pyramid consists of images and its reduced results. Thus, to construct it, we start with the original image and iteratively apply reduction, shrinking the image step by step.

Laplacian Pyramid §

The laplacian pyramid contains the difference between images and their reduced-expanded counterparts; in other words, it contains the information that’s lost from reduction.

To compute one layer in the pyramid, we take the original image, perform reduction and expansion, then subtract the original and the expanded result. The resulting laplacian image highlights edges in the original, which are often useful for downstream applications.

We can compute the entire laplacian pyramid by performing this operation across the gaussian pyramid.

Compression §

Using the laplacian pyramid, we can save an image in a compressed representation. The key idea is that the laplacians have a much smaller range of intensities, which can be quantized or thresholded.

We first compute the gaussian and laplacian pyramids of an image. Then, we only save the final gaussian layer and the entire laplacian layer. To reconstruct, we can recursively expand the gaussian, add the corresponding laplacian, expand again, and so on. Since the laplacian pyramid contains the difference of the gaussian pyramid and reduced-expanded result, this process should accurately reconstruct the entire gaussian pyramid as well as the original image.

The diagram below summarizes the entire construction and reconstruction process. is our original image, and as the subscripts increase, the resolution decreases. The final laplacian layer, unlike the others, is a direct copy of the final gaussian layer. The unlabeled boxes in the center represent additional processing on the laplacian pyramid for whatever task we want to do.