❤️‍🩹 Fault Tolerance

A distributed system at large scale must be able to handle problems smoothly. A fault occurs when some component of the system isn’t working correctly, which can be caused by an infinite number of physical, electrical, or software-related reasons. At scale, these faults are occurring all the time, and we cannot simply stop the system to deal with it.

There are three types of faults:

1. Crash faults: node simply stops due to crash or power loss.
2. Rational behavior: node’s owner manipulates it for some other motive.
3. Byzantine faults: node has arbitrary or malicious behavior.

Moreover, faults may be correlated. For example, if an overloaded machine crashes, the load on other machines increase, potentially leading to more crashes.

To be robust against faults, we can build a service with 🖨️ Replication. Then, a client can send a request to each machine, the machines coordinate and return results, and the client chooses one of the results (like the most common one). The tricky problem here is that we need all machines to process the requests in the same way and same order; otherwise, their states will diverge. To do so, the machines implement a deterministic state machine—here, called state machine replication—and reach a consensus on the processing order.

Consensus §

For consensus, each process can propose a value, and the processes agree on which value to use. Formally, the consensus solution must satisfy:

1. Termination: every correct process eventually decides.
2. Validity: if all processes propose the same value, then every correct process uses that value.
3. Integrity: every correct process decides at most one value, and it can only use values that have been proposed.
4. Agreement: if some correct process decides a value, then every other process must also decide that value.

Unfortunately, the FLIP impossibility result proves that no asynchronous algorithm can achieve consensus in the presence of crash faults. Thus, methods can only guarantee some of the properties above; 🏝️ Paxos is one such example (for crash faults).

Byzantine Fault Tolerance (BFT) §

Byzantine faults are much more difficult to tolerate than crash faults since anything can happen. From here on, we assume that up to nodes are Byzantine.

Byzantine Generals §

Consider the Byzantine Generals problem: we have generals that must agree on a plan, but some of the generals may be traitors. The goal is to have all loyal generals decide on the same plan, and they can communicate with each other.

Each general can learn the opinions of other generals, . Then, it can apply a deterministic function to get the joint decision. However, traitors can send different opinions to different generals, causing the output of to be different; we need some way to ensure that every loyal general uses the same and that if general is loyal, its actual value is used as .

Let’s consider a single opinion; we’ll call the sender the commander, and the recipients are lieutenants. First, we can bound the maximum number of traitors. Consider generals in the figure below:

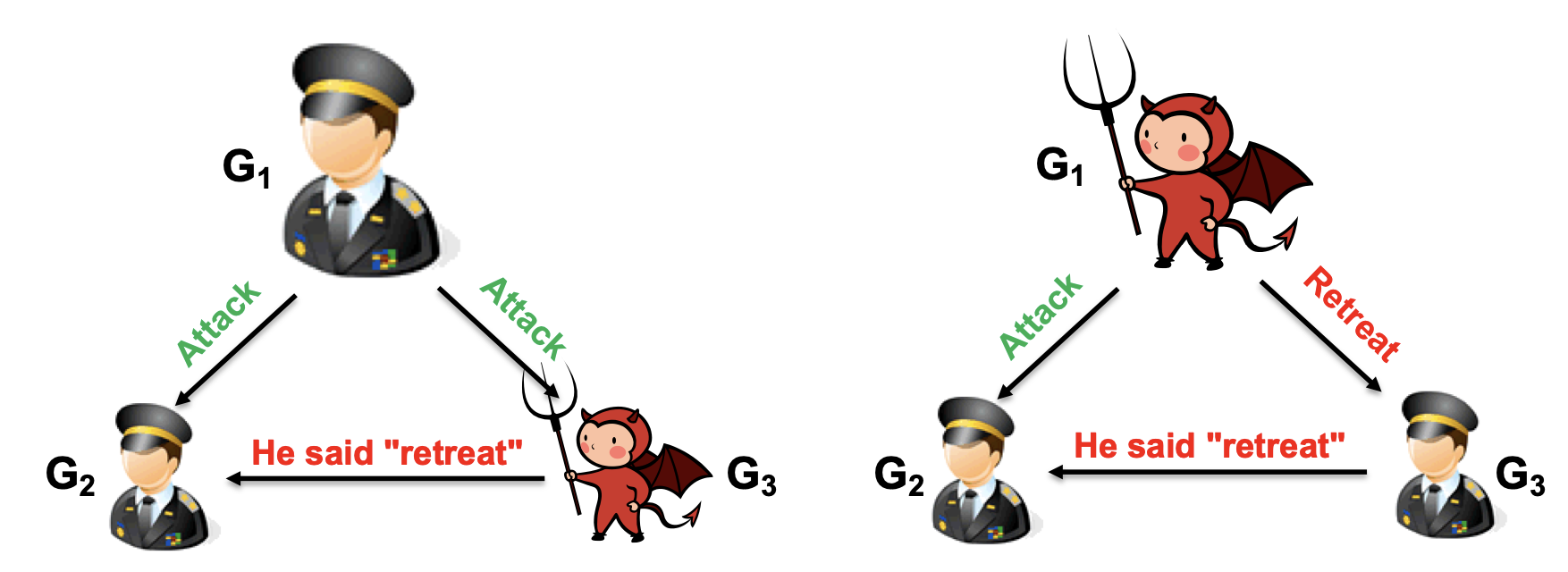
There is no way for to differentiate between these two cases and figure out whether the commander is loyal or not. This same principle can be generalized to larger , showing that we need to tolerate traitors.

With , , there is a solution: let the lieutenants exchange information on what each other heard from the commander. After the exchange, they can go with the command heard most often. Thus, if traitor is a lieutenant, they will be “outvoted” by the other two, and if the traitor is a commander, the lieutenants will have the same information. Let’s call this protocol .

This will not work for , however, since both commander and lieutenant can be traitors and forward duplicate information to every other lieutenant. To resolve this, we observe that the communication between lieutenants is itself the same problem, and we can invoke the protocol recursively. For example, with , the protocol uses to communicate between lieutenants:

1. If the commander is a traitor, there is at most one traitor among the lieutenants and thus reduces to the problem with .
2. If the commander is loyal, can produce a single discrepancy, but since there is at least one loyal lieutenant and commander, the majority will still be correct.

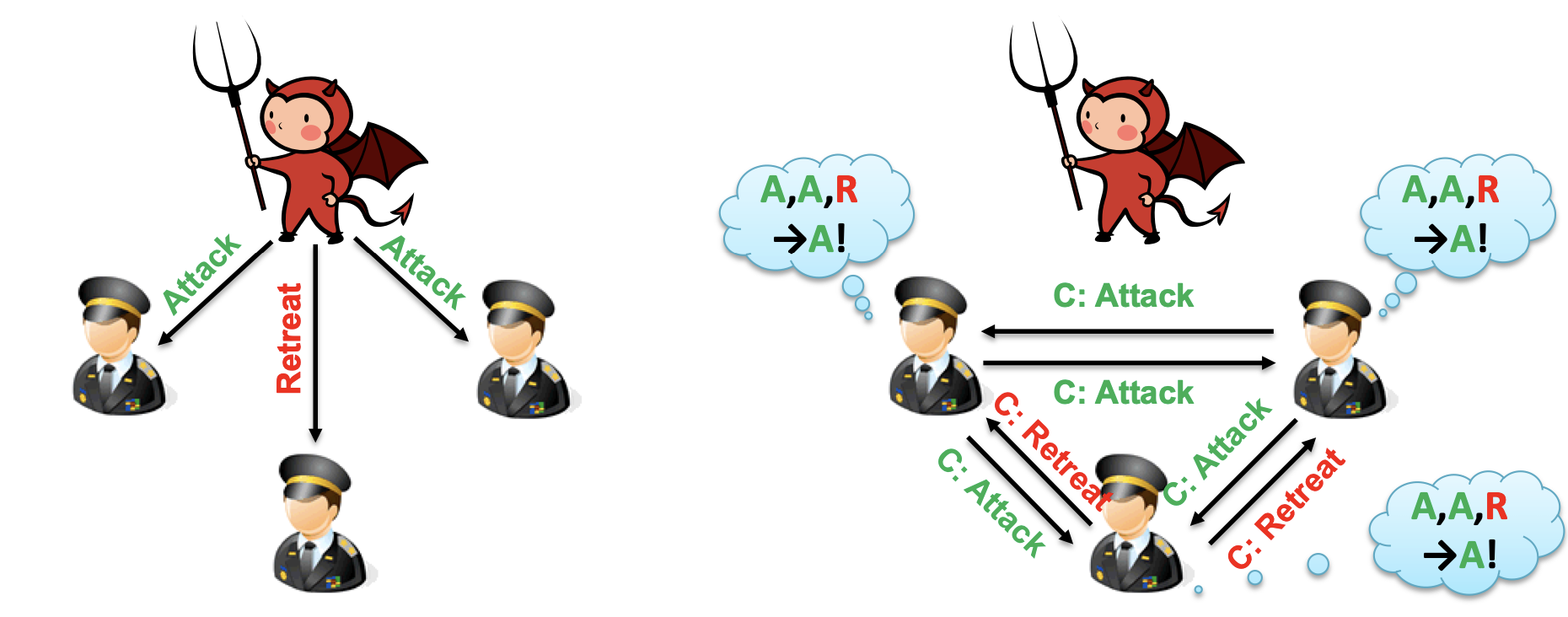
Byzantine Generals with Signatures §

The traitors are a problem because they can change what the commander actually sent when forwarding it to other lieutenants. If we have each general sign their messages, however, then traitors cannot change it.

Now with , the lieutenants can simply exchange messages. If there’s a single command, we go with it; otherwise, the commander sent multiple values and thus is the traitor, so we can choose some default value.

The only problem we have is that with multiple traitors, a traitor commander can send multiple signed values to the traitor lieutenants, which forwards them differently to the other lieutenants. To prevent this, we must ensure that if a signed order is received by a loyal lieutenant, it’s also received by all other loyal lieutenants. To do so, when a lieutenant receives a signed order:

1. If they haven’t seen it before, they add it to their set of valid orders.
2. If the order doesn’t have endorsements from other lieutenants (sent by others), they add their endorsement and sends it to all other lieutenants.

At the end of forwarding, the lieutenants use a deterministic function to pick an order from the set of valid orders. The main idea is that if the commander is a traitor but there are endorsements, then there must be a loyal lieutenant among them that forwarded the order to all lieutenants; if there aren’t enough endorsements, the loyal lieutenant will do it themself.

Application §

With our solution to Byzantine generals, we can ensure consensus in the presence of Byzantine nodes: each node is a general, and the commands are proposals for state-machine replication. The client will send its request to each node, each node proposes some request as the next one to execute, and they use a Byzantine-tolerant protocol to agree on a request; then, they each execute the request and reply to the client, and the client uses the majority response.

PBFT §

PBFT is the classical protocol for this procedure. It uses signatures (as discussed above), but the network is asynchronous—messages can be delayed. Because of this, there’s no way to tell whether a message has been sent is or taking a long time; thus, we need since replicas could be faulty and not respond, and others could respond but also be faulty.

At a high level, it proceeds as follows:

1. Client sends request to primary node.
2. Primary multicasts request to other replicas via a multi-round protocol.
3. Replicas execute request and send responses to client.
4. Client waits for matching responses and uses it as the result.