⏰ Clock Synchronization

Clocks are very useful for a variety of applications (timestamps, deadlines, timeouts, etc.), and generally every machine has a built-in time source. However, the local clock isn’t perfect and will drift—run too slow or too fast—due to finite precision and manufacturing variances.

In a distributed system with multiple nodes and multiple clocks, the drift will cause nodes to have slightly different times—clock skew. This can cause complications for the system; for example, file timestamps will be different across machines, causing confusion.

Thus, we need to synchronize the clocks across nodes; depending on the system’s demands, there are different types of synchronization we can do:

1. Absolute time: wall-clock time, needed for things like scheduled execution.
2. Logical time: an ordering of events—which one happened first?

NTP §

The Network Time Protocol (NTP) is a synchronization algorithm, system architecture, and protocol for synchronizing clocks. The goal is to have one node, the “time server,” that knows the correct time—based on WWV shortwave radio signal or GPS signals, both of which contain the UTC standard—and have other nodes synchronize to the time server’s clock. The key difficulty is that communication between nodes will take time, and we need to account for it.

In NTP, a synchronization request between a node and the time server collects four timestamps: request transmission by client, request arrival by server, response transmission by server, response arrival by client. Note that and are from the same clock, and and are from the same clock.

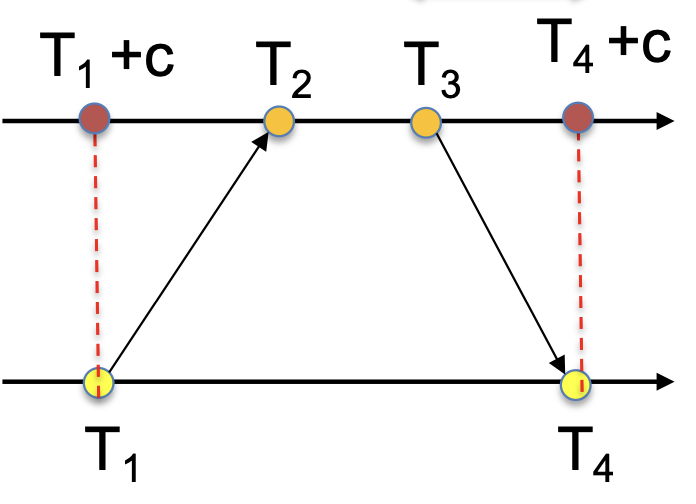
Then, we compute estimates for the time offset to the server,

and the round trip time (RTT),

Based on this, we know that the correct time upon receiving the response is . Instead of setting it directly, which would cause a time jump, we’ll slow down or speed up the node’s clock (depending on the sign of ), allowing it to slowly approach the correct time.

Note that the interaction above is pairwise between the time server and node, which isn’t scalable; for larger systems, we introduce a strata/hierarchy of NTP servers that synchronize across layers. Note that higher strata doesn’t necessarily have better accuracy—it also depends on which servers the node synchronizes with and also the precision of the time source itself.

Finally, NTP has three synchronization modes:

1. Procedure-call mode: one server accepts requests from others (as described above).
2. Multicast mode: one or more servers periodically multicast their time into the network, and receivers set their clock assuming some small delay.
3. Symmetric mode: a pair of servers exchange messages to improve the accuracy of their synchronization. This is used in lower levels of the strata and has the highest accuracy.

Berkeley Algorithm §

In the case that no machine is a good time source, we can still synchronize clocks by averaging them periodically. Since drift is random, we hope that they’ll cancel out.

Periodically, we choose one node as the reference server via election. This node computes a fault-tolerant average by getting each node’s time, plus half the RTT, and calculates the average while ignoring outliers (high RTT or very different time). Finally, this node tells the others the delta between the average and their clock, allowing them to adjust.

Logical Clocks §

Synchronizing the actual time is hard due to delays and limited precision. Sometimes, we only need to order certain events—without knowing their actual time—which is the point of a logical clock.

Lamport Clock §

For events and , we have , or happens before , if:

1. and are events in the same process, and happens before .
2. is the transmission of some message and is its receipt.

If neither nor , then we say and are concurrent.

In a Lamport clock, we aim to assign a time value for each event such that if , . Note that the reverse isn’t true: if , then and can be concurrent. With , if we ever need to decide which of two events come first, we can use the one with lower time value.

To implement a synchronized Lamport clock, each node will have its own simple local clock (which can be a simple increment-only counter). The local clocks don’t need to be synchronized, and the only requirement is that it ticks at least once between events.

When passing messages, the sender of message attaches its time to . Then, the node receiving checks the attached time, and if it’s greater that its local time, the node increases its local time to the attached time.

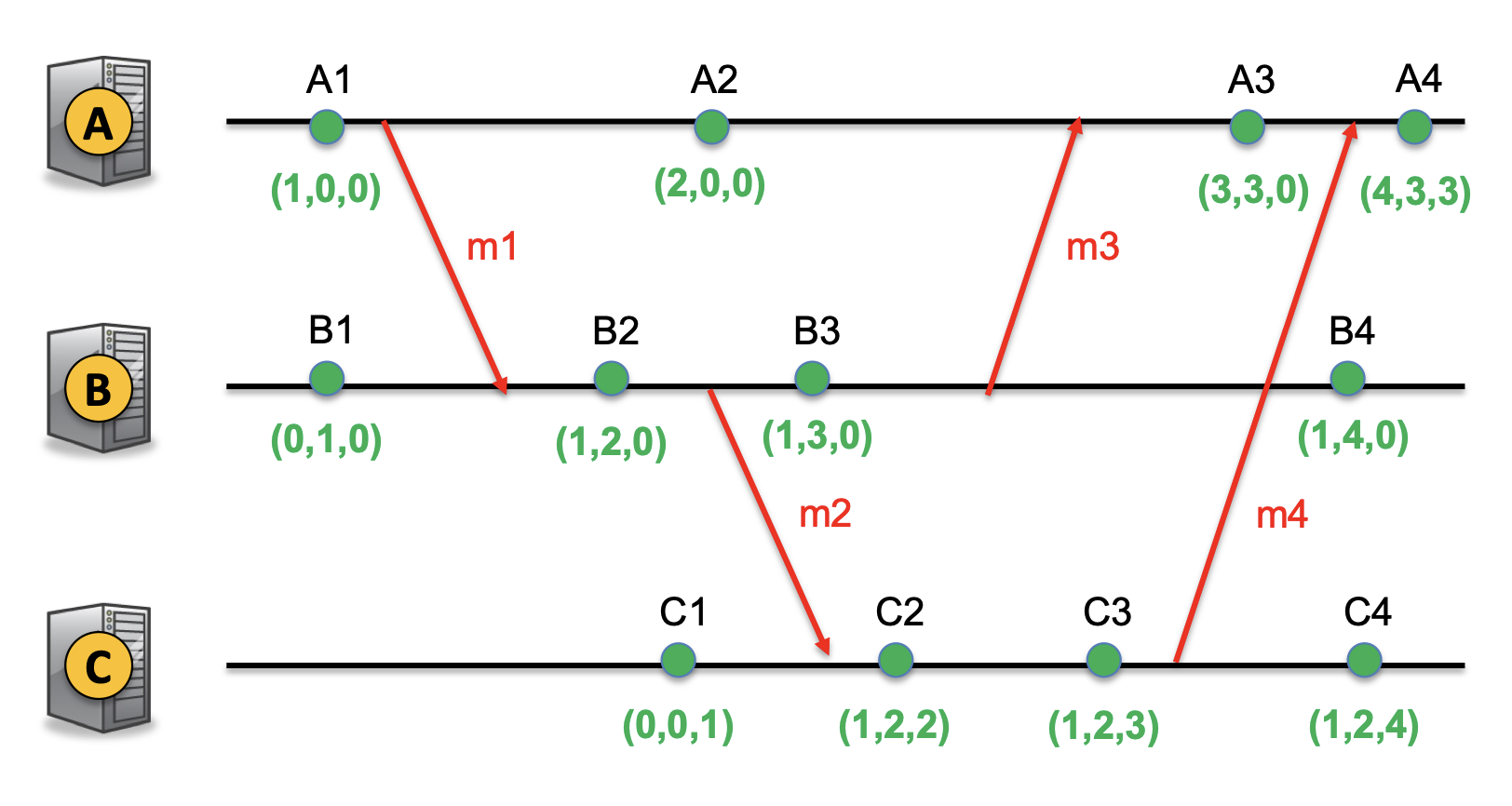
Vector Clock §

In some systems, we want to know what events could have influenced each other (for example, in a distributed database). We can use Lamport clocks for this purpose (ordering changes by Lamport timestamps), but the Lamport clock induces a total event ordering, even on events that didn’t influence each other—if , we don’t know whether . For concurrency, we need a partial ordering that only captures causality.

The solution is a vector clock, which follows the rules below:

1. Each node maintains a vector of clock values, where is the timestamps of the most recent event on that “knows about.”
2. Initially, all values start at , and each node has a local increment-only clock, just like the Lamport clock, that updates .
3. When sends a message , it attaches .
4. When receives message with vector , we set . Intuitively, we can imagine as the latest event the sender knew about for , and so any of these events could have influenced ; then, the recipient knows more about if .

If we have two events and with vectors and , we can order

and vice versa. Otherwise, neither direction is true. An example ordering and is below: